Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\large \mathbb{R}$, và đ

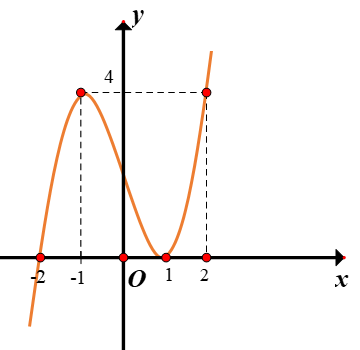
Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\large \mathbb{R}$, và đồ thị của $f'(x)$ trên $\mathbb{R}$ như hình vẽ. Hàm số $y=f(x)$ đồng biến trên khoảng nào?

• A.

  A. $\large (-\infty ;+\infty)$

• B.

  B. $\large (-\infty ;-1)$

• C.

  C. $\large (-2 ;+\infty)$

• D.

  D. $\large (-\infty ; 1)$

Từ đồ thị của $\large y=f^{\prime}(x)$ ta thấy $\large f^{\prime}(x) \geq 0$ khi $\large x \geq-2$. Vậy hàm số đã cho luôn đồng biến trên khoảng $\large (-2 ;+\infty)$

Chọn đáp án C