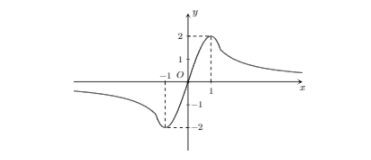
Cho hàm số $\Large y=f(x)$ liên tục trên$\Large \mathbb{R}$ và có đồ t

Cho hàm số $\Large y=f(x)$ liên tục trên$\Large \mathbb{R}$ và có đồ thị như hình dưới 

Biết rằng trục hoành là tiệm cận ngang của đô thị. TÌm tất cả các giá trị thực của tham số m để phương trình $\Large f(x)=4^{m+2\log_{4}\sqrt{2}}$ có hai nghiệm phân biệt dương.

• A.

  A. m > 1

• B.

  B. 0 < m < 1

• C.

  C. m < 0

• D.

  D. 0 < m < 2

Chọn C
Số nghiệm của phương trình $\Large f(x)=4^{m+2\log_{4}\sqrt{2}}$ là số giao điểm của đồ thị hàm số $\Large y=f(x)$ và đường thẳng $\Large y=4^{m+2\log_{4}\sqrt{2}}$

Phương trình có 2 nghiệm phân biệt $\Large \Leftrightarrow 4^{m+2\log_{4}\sqrt{2}}<2\Leftrightarrow 2m+4\log_{4}\sqrt{2}<1\Leftrightarrow m<0$