Cho hàm số $\Large y=f(x)$ liên tục trên $\Large R$. Gọi $\Large {{D}_

Cho hàm số $\Large y=f(x)$ liên tục trên $\Large R$. Gọi $\Large {{D}_{1}}$ là hình phẳng giới hạn bởi đồ thị hàm số $\Large y=f(x)$ , các đường $\Large x=0,x=1$ và trục $\Large Ox$ . Gọi $\Large {{D}_{2}}$ là hình phẳng giới hạn bởi đồ thị hàm số $\Large y=2f(x)$ , các đường $\Large x=0,x=1$ và trục $\Large Ox$ . Quay các hình phẳng $\Large {{D}_{1}}$,$\Large {{D}_{2}}$ quanh trục $\Large Ox$ ta được khối tròn xoay có thể tích lần lượt là $\Large {{V}_{1}},{{V}_{2}}$ . Khẳng định nào sau đây là đúng ?

• A.

  $\Large {{V}_{2}}={{V}_{1}}$

• B.

  $\Large {{V}_{2}}=2{{V}_{1}}$

• C.

  $\Large {{V}_{2}}=4{{V}_{1}}$

• D.

  $\Large {{V}_{2}}=8{{V}_{1}}$

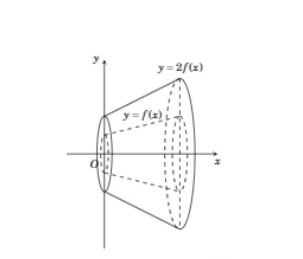
Ta có $\Large {{V}_{1}}=\int\limits_{0}^{1}{\pi {{f}^{2}}(x)dx}$

$\Large {{V}_{2}}=\int\limits_{0}^{1}{\pi {{(2f(x))}^{2}}dx=4\int\limits_{0}^{1}{\pi {{f}^{2}}(x)dx=4{{V}_{1}}}}$

Chọn đáp án C