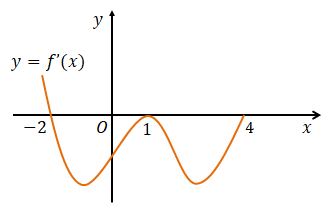
Cho hàm số $\Large y=f(x)$ . Hàm số $\Large y={f}'(x)$ có đồ thị như h

Cho hàm số $\Large y=f(x)$ . Hàm số $\Large y={f}'(x)$ có đồ thị như hình bên . Biết rằng diện tích hình phẳng giới hạn bởi trục $\Large Ox$ và đồ thị hàm số $\Large y={f}'(x)$ trên đoạn $\Large [-2;1]$ và $\Large[1;4]$ lần lượt bằng 9 và 12 . Cho $\Large f(1)=3$ . Giá trị của biểu thức $\Large f(-2)+f(4)$ bằng

• A.

  $\Large 21$

• B.

  $\Large 9$

• C.

  $\Large 3$

• D.

  $\Large 2$

Dựa vào đồ thị hàm số, kết hợp với giả thiết ta có:

$\Large \int\limits_{-2}^{1}{{f}'(x)dx=-9\Rightarrow f(1)-f(-2)=-9\Rightarrow f(-2)=9+f(1)=12}$

$\Large \int\limits_{1}^{4}{{f}'(x)dx=-12\Rightarrow f(4)-f(1)=-12\Rightarrow f(4)=-12+f(1)=-9}$

Vậy $\Large f(-2)+f(4)=3$

Chọn đáp án C