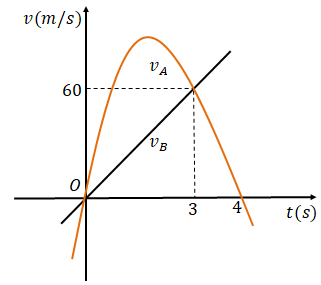
Cho đồ thị biểu thị vận tốc của hai xe A và B khởi hành cùng một lúc ,

Cho đồ thị biểu thị vận tốc của hai xe A và B khởi hành cùng một lúc , bên cạnh nhau và trên cùng một con đường . Biết đồ thị biểu diễn vận tốc của xe A là một đường parabol, đồ thị biểu diễn vận tốc của xe B là một đường thẳng (như hình vẽ) . Hỏi sau khi đi được 3 giây, khoảng cách giữa hai xe là bao nhiêu mét ? 

• A.

  $\Large 90m$

• B.

  $\Large 60m$

• C.

  $\Large 0m$

• D.

  $\Large 270m$

Phương trình vận tốc của xe A có dạng $\Large v(t)=a{{t}^{2}}+bt+c$

Dựa vào đồ thị ta có: $\Large \left\{ \begin{align}  & v(0)=0 \\  & v(3)=60 \\  & v(4)=0 \\ \end{align} \right.$ $\Large \Leftrightarrow \left\{ \begin{align}  & c=0 \\  & 9a+3b+c=60 \\  & 16a+4b+c=0 \\ \end{align} \right.$ $\Large \Leftrightarrow \left\{ \begin{align}  & a=-20 \\  & b=80 \\  & c=0 \\ \end{align} \right.$ 

$\Large \Rightarrow v(t)=-20{{t}^{2}}+80t$ suy ra quãng đường xe A đi được trong 3 giây đầu là $\Large {{s}_{A}}=\int\limits_{0}^{3}{v(t)dt=\int\limits_{0}^{3}{(-20{{t}^{2}}+80t)dt=180(m)}}$

Vận tốc xe B có phương trình là $\Large v(t)=20t$ , sau 3 giây, xe B đi được quãng đường là 

$\Large {{s}_{B}}=\int\limits_{0}^{3}{20tdt=10{{t}^{2}}\left| \begin{align}  & 3 \\  & 0 \\ \end{align} \right.=90(m)}$

Vậy sau khi đi được 3 giây, hai xe cách nhau là $\Large 180-90=90(m)$