Cho hàm số $\large y=f(x)$ có đồ thị như hình bên. Gọi k, K lần lượt l

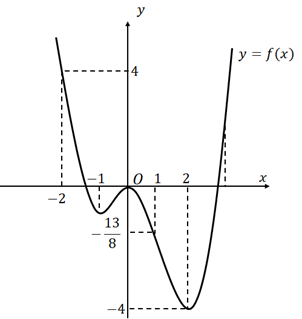
Cho hàm số $\large y=f(x)$ có đồ thị như hình bên. Gọi k, K lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số $\large y=f(-2x)$ trên đoạn $\large \left[-1; \dfrac{1}{2}\right]$. Giá trị $\large k+K$ bằng

• A. $\large 0$
• B. $\large \dfrac{19}{8}$
• C. $\large 4$
• D. $\large -4$

Đặt $\large t=-2x, x\in \left[-1; \dfrac{1}{2} \right ]\Rightarrow t=-2x\in [-1; 2]$

Dựa vào đồ thị ta có: $\large \left\{\begin{align}& K=\underset{x\in \left[-1; \dfrac{1}{2} \right ]}{\max} f(-2x)=\underset{t\in[-1; 2]}{\max}f(t)=0\\& k=\underset{x\in\left[-1; \dfrac{1}{2} \right ]}{\min} f(-2x)=\underset{t\in [-1; 2]}{\min} f(t)=-4\\\end{align}\right.$

Vậy $\large k+K=-4$