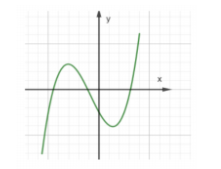
Cho hàm số $\large y = ax^{3} + bx^{2} + cx + d$ có đồ thị như hình vẽ

Cho hàm số $\large y = ax^{3} + bx^{2} + cx + d$ có đồ thị như hình vẽ. Trong các số $\large a,b, c, d$ có bao nhiêu số dương ? 

• A.

  1

• B.

  4

• C.

  3

• D.

  2

Từ hình dạng đồ thị hàm số ta có $\large a > 0$
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm $\large \Rightarrow d < 0$
Ta có: $\large y' = 3ax^{2} + 2bx + c$
Hàm số có hai điểm cực trị trái dấu $\large \Rightarrow y' = 0$ có hai nghiệm trái dấu $\large \Leftrightarrow ca < 0$
Mà $\large a > 0$ nên $\large c < 0$
Ta lại có: $\large y'' = 6ax + 2b$
$\large y'' = 0 \Leftrightarrow 6ax + 2b = 0 \Leftrightarrow x = \dfrac {-b}{3a}$
Từ đồ thị hàm số ta thấy tâm đối xứng có hoành độ âm. Do đó: $\large \dfrac {-b}{3a} < 0$
Mà $\large a > 0$ nên $\large b > 0$
Vậy trong các số $\large a,b, c, d$ có 2 số dương $\large a,b$