Cho hàm số $\Large f(x)$ xác định trên $\Large \mathbb{R} \setminus \b

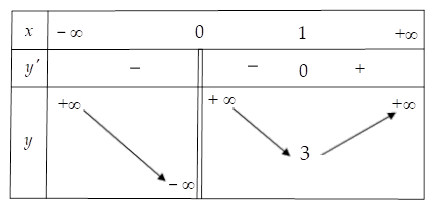
Cho hàm số $\Large f(x)$ xác định trên $\Large \mathbb{R} \setminus \begin{Bmatrix}
0
\end{Bmatrix}$ và có bảng biến thiên như hình vẽ.

Số nghiệm của phương trình $\Large 3|f(2x-1)|-10=0$ là

• A. 2.
• B. 1.
• C. 4.
• D. 3.

Chọn C

Đặt $\Large t=2x-1$, ta có phương trình trở thành $\Large |f(t)|=\dfrac{10}{3}$. Với mỗi nghiệm t thì có một nghiệm $\Large x=\dfrac{t+1}{2}$ nên số nghiệm t của phương trình $\Large |f(t)|=\dfrac{10}{3}$ bằng số nghiệm của $\Large 3|f(2x-1)|-10=0$.

Bảng biến thiên của hàm số $\Large y=|f(x)|$ là

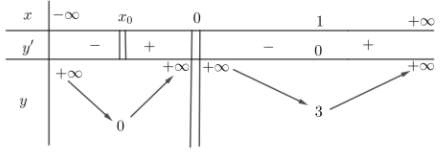
Suy ra phương trình $\Large |f(t)|=\dfrac{10}{3}$ có 4 nghiệm phân biệt nên phương trình $\Large 3|f(2x-1)|-10=0$ có 4 nghiệm phân biệt.