Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi O và O' lần lượt

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi O và O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. Gọi M, N lần lượt là trung điểm của các cạnh B'C' và CD. Tính thể tích khối tứ diện OO'MN.

• A.

  $\Large \dfrac{a^3}{8}.$

• B.

  $\Large a^3.$

• C.

  $\Large \dfrac{a^3}{12}.$

• D.

  $\Large \dfrac{a^3}{24}.$

Chọn D

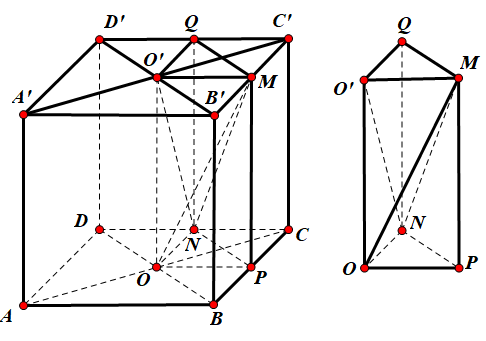
Gọi P, Q lần lượt là trung điểm của BC và C'D'.

Ta có $\Large S_{\Delta OPN}=\dfrac{1}{4}S_{\Delta BCD}=\dfrac{1}{8}S_{ABCD}=\dfrac{a^2}{8} \Rightarrow V_{OPN.{O}'MQ}=\dfrac{a^3}{8}$.

Mà $\Large V_{O{O}'MN}=V_{OPN.{O}'MQ}-V_{M.OPN}-V_{N.{O}'MQ}=\dfrac{a^3}{8}-\dfrac{1}{3}.\dfrac{a^3}{8}-\dfrac{1}{3}.\dfrac{a^3}{8}=\dfrac{a^3}{24}$.