Trong không gian $\Large Oxyz$, cho mặt cầu $\Large (S): (x-1)^2+(y+2)

Trong không gian $\Large Oxyz$, cho mặt cầu $\Large (S): (x-1)^2+(y+2)^2+(z-3)^2=12$ và mặt phẳng $\Large (P): 2x+2y-z-1=0$. Mặt phẳng $\Large (Q)$ song song với $\Large (P)$ và cắt $\Large (S)$ theo thiết diện là một đường tròn $\Large (C)$ sao cho khối nón có đỉnh là tâm mặt cầu và đáy là hình tròn $\Large (C)$ có thể tích lớn nhất. Mặt phẳng $\Large (Q)$ có phương trình là

 

• A. $\Large 2x+2y-z+2=0$.
• B. $\Large 2x+2y-z+8=0$.
• C. $\Large 2x+2y-z+3=0$.
• D. $\Large 2x+2y-z+11=0$.

Chọn D

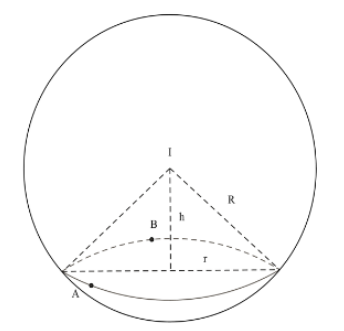
Mặt cầu $\Large (S)$ có tâm $\Large I(1; -2; 3)$, bán kính $\Large R=2\sqrt{3}$.

Do $\Large (Q)$ song song với $\Large (P)$ nên $\Large (Q): 2x+2y-z+d=0$, $\Large (d\neq -1)$.

Gọi $\Large r$ là bán kính của hình tròn $\Large (C)$. Khi đó khối nón có đỉnh là tâm mặt cầu và đáy là hình tròn $\Large (C)$ có thể tích là $\Large V=\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}\pi (R^2-h^2)h$ với $\Large h$ là chiều cao của khối nón trên.

Theo bất đẳng thức Cô-si ta có:

$\Large V^2=\dfrac{1}{9}\pi^2(R^2-h^2)^2h^2$ $\Large =\dfrac{1}{18}\pi^2(R^2-h^2)(R^2-h^2)(2h^2)$$\Large \leq \dfrac{1}{18}\pi^2.\left(\dfrac{(R^2-h^2)+(R^2-h^2)+(2h^2)}{3}\right)^3$

Suy ra $\Large V\leq \dfrac{2\pi R^3}{9\sqrt{3}}=\dfrac{16\pi}{3}$.

Vậy $\Large \max V=\dfrac{16\pi}{3}$ $\Large \Leftrightarrow R^2-h^2=2h^2$ $\Large \Leftrightarrow h=\dfrac{R}{\sqrt{3}}=2$.

Khi đó $\Large d\left(I, (Q)\right)=2$ $\Large \Leftrightarrow \dfrac{|2-4-3+d|}{3}=2$ $\Large \Leftrightarrow |d-5|=6$ $\Large \Leftrightarrow \left[\begin{align} & d=11\\ & d=-1\end{align}\right.$. Đổi chiếu điều kiện $\Large d\neq -1$ ta được $\Large d=11$.

Vậy $\Large (Q): 2x+2y-z+11=0$.