Cho hai số thực a,ba,b lớn hơn 1. Tìm giá trị nhỏ nhất của biểu

MỤC LỤC
Câu hỏi:
Cho hai số thực a,ba,b lớn hơn 1. Tìm giá trị nhỏ nhất của biểu thức S=loga(a2+4b24)+14logabbS=loga(a2+4b24)+14logabb.
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
Theo bất đẳng thức Côsi ta có a2+4b24=a2+(2b)24≥4ab4a2+4b24=a2+(2b)24≥4ab4 ⇒loga(a2+4b24)≥logaab⇒loga(a2+4b24)≥logaab.
Do a,b>1a,b>1 ⇒logab>loga1=0⇒logab>loga1=0.
Ta có
S=loga(a2+4b24)+14logbab≥logaab+14logbabS=loga(a2+4b24)+14logbab≥logaab+14logbab
=1+logab+14(logba+1)=logab+14logab+54=1+logab+14(logba+1)=logab+14logab+54.
Đặt t=logabt=logab, ta có S≥t+14t+54S≥t+14t+54.
Xét hàm số f(t)=t+14t+54f(t)=t+14t+54 với t>0t>0.
Ta có f′(t)=1−14t2=4t2−14t2.
Khi đó f′(t)=0 ⇔4t2−14t2=0 ⇔4t2−1=0 ⇔t2=14 ⇒t=12.
Bảng biến thiên
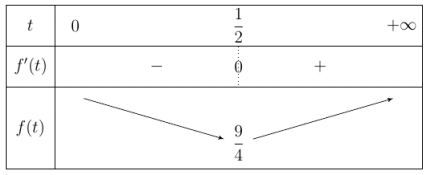
Suy ra mint∈(0;+∞)f(t)=94 khi t=12.
Vậy giá trị nhỏ nhất của S=94 khi t=logab=12 ⇔b=√a.
Xem thêm các bài tiếp theo bên dưới