Cho bốn hàm số $\Large y=\left(\dfrac{1}{\sqrt{2}}\right)^x (1), y=3^x

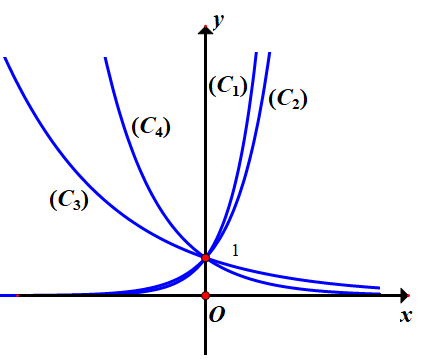
Cho bốn hàm số $\Large y=\left(\dfrac{1}{\sqrt{2}}\right)^x  (1), y=3^x (2), y=\left(\dfrac{1}{2}\right)^x (3), y=4^x  (4)$ và bốn đường cong $\Large (C_{1}), (C_{2}), (C_{3}), (C_{4})$ như hình vẽ. Đồ thị hàm số (1), (2), (3), (4) lần lượt là 

• A.

  A. $\Large (C_{1}), (C_{2}), (C_{3}), (C_{4})$

• B.

  B. $\Large (C_{3}), (C_{2}), (C_{4}), (C_{1})$

• C.

  C. $\Large (C_{2}), (C_{4}), (C_{1}), (C_{3})$

• D.

  D. $\Large (C_{4}), (C_{1}), (C_{3}), (C_{2})$

Chọn B

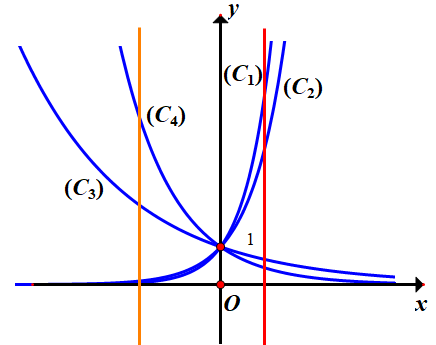
Đồ thị hàm số $\Large (C_{3}), (C_{4})$ đi từ trái sang phải theo chiều hướng xuống nên là những hàm số nghịch biến $\Large \rightarrow (C_{3}), (C_{4})$ tương ứng với (1) hoặc (3)

Từ đồ thị hàm số ta thấy tại cùng một giá trị $\Large x_{0}<0$ thì đồ thị hàm số $\Large (C_{4})$ nằm trên đồ thị hàm số $\Large (C_{3})$. Chọn $\Large x_{0}=-1\rightarrow \left(\dfrac{1}{2}\right)^{-1}>\left(\dfrac{1}{\sqrt{2}}\right)^{-1}$. Do đó: $\Large (C_{4})\leftrightarrow (3); (C_{3})\leftrightarrow (1)$

Tương tự: $\Large (C_{1})\leftrightarrow (4); (C_{2})\leftrightarrow (2)$