Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện

Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng $\Large 3a$. Tính diện tích toàn phần của hình trụ đã cho.

• A. $\Large \dfrac{13\pi {{a}^{2}}}{6}$.
• B. $\Large \dfrac{27\pi {{a}^{2}}}{2}$.
• C. $\Large 9\pi {{a}^{2}}$.
• D. $\Large \dfrac{9\pi {{a}^{2}}}{2}$.

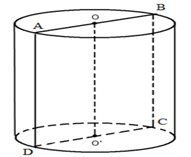
Gọi thiết diện qua trục là hình vuông $\Large ABCD$. Theo đề thì $\Large AB=AD=3a$.

Bán kính đáy của hình trụ là $\Large \Large R=\dfrac{AB}{2}=\dfrac{3a}{2}$\Large .

Đường sinh của hình trụ là $\Large \Large l=AD=3a$\Large .

Áp dụng công thức diện tích toàn phần của hình trụ, ta có $\Large {{S}_{tp}}=2\pi Rl+2\pi {{R}^{2}}=2\pi .\dfrac{3a}{2}.3a+2\pi {{\left( \dfrac{3a}{2} \right)}^{2}}=\dfrac{27\pi {{a}^{2}}}{2}$.