Các đoạn AM, MN, NB lần lượt chứa các phần tử: cuộn cảm thuần, điện tr
MỤC LỤC
Câu hỏi:
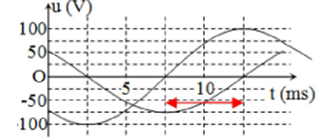
Các đoạn AM, MN, NB lần lượt chứa các phần tử: cuộn cảm thuần, điện trở, tụ điện. Dòng điện xoay chiều chạy qua mạch có tần số ổn định và có giá trị cực đại là 1A. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hai đầu đoạn mạch AN và hai đầu đoạn mạch MB theo thời gian t. Giá trị hệ số tự cảm của cuộn dây và điện dung của tụ điện lần lượt là

Đáp án án đúng là: D
Lời giải chi tiết:
Phương pháp:
+ Đọc đồ thị
+ Sử dụng biểu thức: U=IZU=IZ
+ Vận dụng giản đồ véc-tơ
Cách giải:
Từ đồ thị, ta có:
+ T2=10ms⇒T=20ms⇒ω=2πT=100π(rad/s)T2=10ms⇒T=20ms⇒ω=2πT=100π(rad/s)
+ U0AN=100V=√U20R+U20LU0AN=100V=√U20R+U20L và U0MB=75V=√U20R+U20CU0MB=75V=√U20R+U20C
Tại t=0:t=0: {uAN=−75V=−34U0ANuMB=50V=23U0MB ⇒uAN⊥uMB
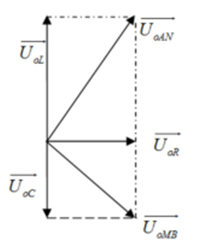
⇒1U20R=1U20AN+1U20MB⇒U0R=60V⇒ {U0L=80VU0C=45V
- Cảm kháng: ZL=U0LI0=80Ω⇒L=ZLω=80100π=254,65mH
- Dung kháng: ZC=U0CI=45Ω⇒C=1ZC.ω=70,735.10−6F
Chọn D.
Xem thêm các bài tiếp theo bên dưới
- Một sóng ngang có bước sóng truyền trên sợi dây dài, qua điểm M rồi đế
- Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần
- Cần truyền tải điện từ nhà máy đến nơi tiêu thụ điện sao cho công suất
- Cho mạch điện có sơ đồ như hình vẽ: $\large E=8V; r=2,0\Omega; R_1=12\
- Đặt điện áp xoay chiều có giá trị hiệu dụng 220V vào hai đầu hộp đen X