Cho mạch điện có sơ đồ như hình vẽ: $\large E=8V; r=2,0\Omega; R_1=12\

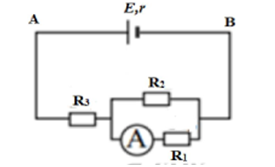
Cho mạch điện có sơ đồ như hình vẽ:  $\large E=8V; r=2,0\Omega; R_1=12\Omega; R_2=6\Omega$. Bỏ qua điện trở của ampe kế và dây nối. Số chỉ của ampe kế là $\large 0,33\approx\dfrac{1}{3}A$.  Nhiệt lượng tỏa ra trên $\large R_3$ trong 10 phút là 

• A. A. 5,4kJ
• B. B. 1,8kJ
• C. C. 9,6kJ
• D. D. 2,4kJ

Phương pháp: 
+ Sử dụng biểu thức của đoạn mạch mắc song song, nối tiếp 
+ Sử dụng biểu thức định luật ôm cho toàn mạch: $\large I=\dfrac{E}{R_N+r}$
+ Sử dụng biểu thức tính nhiệt lượng tỏa ra: $\large Q=I^2Rt$  
Cách giải: 
+  $\large I_A=I_1=\dfrac{1}{3}A\Rightarrow U_1=I_1R_1=\dfrac{1}{3}.12=4V$
Lại có: $\large U_{12}=U_1=U_2$ 
 $\large I_{12}=I=\dfrac{U_{12}}{R_{12}}$ và  $\large R_{12}=\dfrac{R_1R_2}{R_1+R_2}=4\Omega\Rightarrow I=\dfrac{4}{4}=1A$
Mặt khác: $\large I=\dfrac{E}{R_N+r}\Leftrightarrow 1=\dfrac{8}{R_N+1}\Rightarrow R_N=7\Omega$ 
+ Điện trở mạch ngoài: $\large R_N=\dfrac{R_1R_2}{R_1+R_2}+R_3=7\Omega\Rightarrow R_3=3\Omega$ 
Nhiệt lượng tỏa ra trên $\large R_3$ trong $\large t=10'=600s$ là: $\large Q=I^2, R_3t=1^2.3.600=1800 J=1,8 kJ$ 
Chọn B.