Người ta định đầu tư một phòng hát Karaoke hình hộp chữ nhật có diện t

Người ta định đầu tư một phòng hát Karaoke hình hộp chữ nhật có diện tích sàn khoảng $\large 18m^2$ cao 3m. Dàn âm thanh gồm 4 loa có công suất như nhau đặt tại các góc dưới A, B và các góc A', B' ngay trên A, B, màn hình gắn trên tường ABA'B'. Bỏ qua kích thước của người và loa, coi rằng loa phát âm đẳng hướng và tường hấp thụ âm tốt. Phòng có thiết kế để công suất đến tai người ngồi hát tại trung điểm M của CD đối diện cạnh AB là lớn nhất. Tai người chịu được cường độ âm tối đa bằng  $\large 9W/m^2$. Công suất lớn nhất của mỗi loa mà tai người còn chịu đựng được gần giá trị nào sau đây 

• A. A. 535W
• B. B. 814W
• C. C. 543W
• D. D. 678W

Phương pháp: 
+ Sử dụng biểu thức tính cường độ âm: $\large I=\dfrac{P}{4\pi r^2}$
+ Sử dụng BĐT Cosi 
Cách giải: 

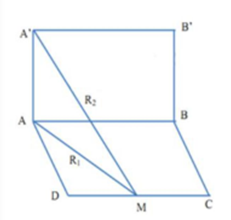
+ Gọi P là công suất của mỗi loa 
Cường độ âm tại M: $\large I=I_A+I_B+I_{A'}+I_{B'}=2(I_1+I_2)$
Với $\large \left\{\begin{align}& I_1=I_A=I_B=\dfrac{P}{4\pi R^2_1}\\& I_2=I_{A'}=I_{B'}=\dfrac{P}{4\pi R_2^2}\\\end{align}\right.$ 
Đặt $\large \left\{\begin{align}& AD=a\\& CD=b\\\end{align}\right.$ ta có: $\large ab=18m^2$
$\large R^2_1=a^2+\dfrac{b^2}{4}$ và $\large R_2^2=R_1^2+AA'^2=a^2+\dfrac{b^2}{4}+9$ 
$\large P=P_{max}$ khi $\large I_1, I_2$ có giá trị lớn nhất tức là khi $\large R_1$ có giá trị nhỏ nhất 
Theo BĐT Cosi, ta có: $\large R_1^2=a^2+\dfrac{b^2}{4}\geq 2a. \dfrac{b}{2}=ab=18$
$\large \Rightarrow$ Giá trị nhỏ nhất của $\large R_1^2=18 m^2$ khi $\large a=\dfrac{b}{2}=3 m$ và  $\large R_2^2=18+9=27 m^2$
Khi đó: $\large \left\{\begin{align}& I_1=\dfrac{P}{72\pi}\\& I_2=\dfrac{P}{108\pi}\\\end{align}\right.$ $\large \Rightarrow I=2(I_1+I_2)=\dfrac{5P}{108\pi}=8(W/m^2)\Rightarrow P_{min}=542,87 W$
Chọn C.