Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần

Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số $\large x_1=2\cos\left(2\pi t-\dfrac{\pi}{3}\right) cm; x_2=2\cos(2\pi t) cm$ .Tốc độ trung bình của vật từ lúc bắt đầu chuyển động đến khi vật qua vị trí có động năng bằng thế năng lần thứ nhất là 

• A. A. 4,098cm/s
• B. B. 7,098cm/s
• C. C. 6,24cm/s
• D. D. 5,027cm/s

Phương pháp: 
+ Tổng hợp dao động: $\large x=x_1+x_2$
+ Vận dụng biểu thức tính tốc độ trung bình: $\large v_{tb}=\dfrac{S}{t}$ 
Cách giải: 
+ Dao động tổng hợp: $\large x=x_1+x_2=2\angle -\dfrac{\pi}{3}+2\angle 0=2\sqrt{3}\angle -\dfrac{\pi}{6}\Rightarrow x=2\sqrt{3}\cos\left(2\pi t-\dfrac{\pi}{6} \right ) cm$ 
+ Tại thời điểm ban đầu: $\large \left\{\begin{align}& x_0=2\sqrt{3}\cos\left(-\dfrac{\pi}{6}\right)=\dfrac{A\sqrt{3}}{2}\\& v_0=-A\omega\sin\left(-\dfrac{\pi}{6}\right)\\\end{align}\right.$  
+ Tại vị trí có $\large W_d=W_t\Rightarrow x=\pm \dfrac{A}{\sqrt{2}}$
Vẽ trên trục thời gian ta được:

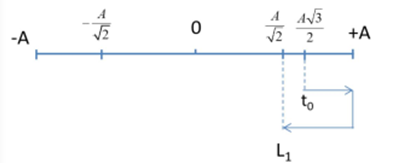
+ Quãng đường vật đi được trong thời gian đó là:  $\large S=\left(A-\dfrac{A\sqrt{3}}{2} \right )+\left(A-\dfrac{A}{\sqrt{2}} \right )=4\sqrt{3}-3-\sqrt{6} (cm)$
+ Thời gian vật đi được khi đó: $\large \Delta t=\dfrac{T}{12}+\dfrac{T}{8}=\dfrac{5T}{24}=\dfrac{5}{24}s$ 
Tốc độ trung bình của vật trong khoảng thời gian đó: $\large v_{tb}=\dfrac{S}{t}=\dfrac{4\sqrt{3}-3-\sqrt{6}}{\dfrac{5}{24}}=7,0978 cm/s$ 
Chọn B.