Biết rằng hàm số $\Large y=f(x)=a x^{4}+b x^{2}+c$ có đồ thị là đường

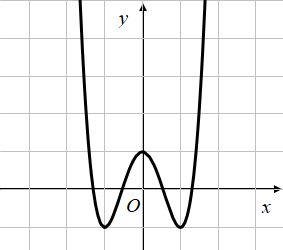
Biết rằng hàm số $\Large y=f(x)=a x^{4}+b x^{2}+c$ có đồ thị là đường cong trong hình vẽ dưới đây

Tính $\Large a+b+2c$

• A. 1
• B. 0
• C. -1
• D. -2

$\Large y^{\prime}=f^{\prime}(x)=4 a x^{3}+2 b x$

Đườngc ong cắt trục Oy tại $\Large M(0 ; 1) \Rightarrow c=1$

Hàm số đạt cực trị tại $\Large x=-1$ và $\Large x=1$ ta có:

$\Large \begin{array}{l}
f^{\prime}(-1)=f^{\prime}(1)=0 \\
\Leftrightarrow 4 a+2 b=0(1)
\end{array}$

Hàm số đi qua $\Large A(-1 ;-1) ; B(1 ;-1)$ ta có:

$\Large \begin{aligned}
&f(-1)=f(1)=-1\\
&\Leftrightarrow a+b+1=-1
\end{aligned}$

Từ (1) và (2) ta có hệ 

$\Large \left\{\begin{array}{l}
4 a+2 b=0 \\
a+b+1=-1
\end{array}\right.\Leftrightarrow\left\{\begin{array}{l}
a=2 \\
b=-4
\end{array}\right.$

Vậy $\Large a+b+2 c=0$