Bảng biến thiên sau là của hàm số nào dưới đây? A. $\large y=\dfrac{1}

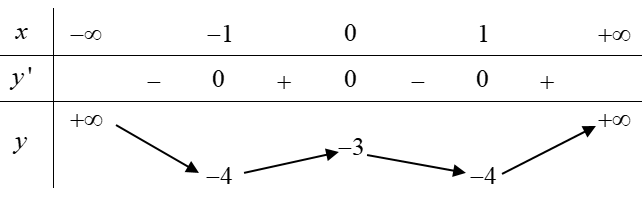
Bảng biến thiên sau là của hàm số nào dưới đây?

• A.

  A. $\large y=\dfrac{1}{2} x^{4}-x^{2}-3$

• B.

  B. $\large y=2 x^{4}-4 x^{2}-3$

• C.

  C. $\large y=2|x|^{3}-3|x|-3$

• D.

  D. $\large y=2\left|x^{3}\right|-3 x^{2}-3$

Chọn D

Phương pháp:

Dựa vào bảng biến thiên, thay các điểm thuộc đồ thị hàm số vào các hàm số ở các đáp án để loại dần các đáp án.

Cách giải:

Dựa vào BBT ta thấy hàm số cần tìm có đồ thị đi qua các điểm (-1;-4),(0;-3),(1;-4)

Thay tọa độ điểm (-1;-4) vào công thức các hàm số ta loại trừ được đáp án A và B.

+) Đáp án C: Ta có: $\large y=2|x|^{3}-3|x|-3=\left\{\begin{array}{l}
2 x^{3}-3 x-3 \text { khi } x \geq 0 \\
-2 x^{3}+3 x-3 \text { khi } x<0
\end{array}\right.$

Xét hàm số: $\large y=2 x^{3}-3 x-3$ có $\large y^{\prime}=6 x^{2}-3 \Rightarrow$ $\large y^{\prime}=0 \Leftrightarrow 6 x^{2}-3=0 \Leftrightarrow$ $\large x=\pm \dfrac{\sqrt{2}}{2} \Rightarrow x=\dfrac{\sqrt{2}}{2}$ (do $\large x \geq 0$) $\large \Rightarrow$ Suy ra hàm số có một điểm cực trị $\large x=\dfrac{\sqrt{2}}{2}$

Mặt khác dựa vào BBT ta có hàm số có 3 điểm cực trị $\large x=-1, x=0, x=1 \Rightarrow$ loại đáp án C.

Suy ra đáp án cần chọn: D