Bắn một proton vào hạt nhân $\Large\mathrm{_3^7Li}$ đứng yên. Phản ứng

Bắn một proton vào hạt nhân $\Large\mathrm{_3^7Li}$ đứng yên. Phản ứng tạo ra hai hạt nhân X giống nhau bay ra với cùng tốc độ và theo các phương hợp với phương tới của proton các góc bằng nhau $60^{\circ}$. Lấy khối lượng của mỗi hạt nhân tính theo đơn vị u bằng số khối của nó. Tỉ số giữa tốc độ của proton và tốc độ của hạt nhân X là

• A. 4
• B. 2
• C. 1/4
• D. 1/2

Phương pháp: Sử dụng định luật bảo toàn điện tích và số khối để viết phương trình phản ứng. Sử dụng định luật bảo toàn động lượng. 
Cách giải: 
Phương trình phản ứng
$\Large\mathrm{{ }_{1}^{1} p}+{ }_{3}^{7} \mathrm{Li} \rightarrow{ }_{2}^{4} \mathrm{X}+{ }_{2}^{4} \mathrm{X}$
Ta có: $\Large\overline{\mathrm{p}_{\mathrm{p}}}=\overline{\mathrm{p}_{\mathrm{x}}}+\overline{\mathrm{p_X}}$
 
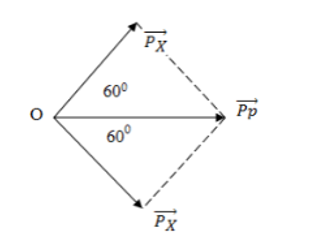
Từ hình vẽ ta có $\Large\Delta \mathrm{OP}_{\mathrm{X}} \mathrm{P}_{\mathrm{p}}$ là tam giác đều $\Large\Rightarrow \mathrm{p}_{\mathrm{X}}=\mathrm{p}_{\mathrm{p}} \Leftrightarrow \mathrm{m}_{\mathrm{X}} \mathrm{v}_{\mathrm{X}}=\mathrm{m}_{\mathrm{p}} \mathrm{v}_{\mathrm{p}} \Rightarrow \dfrac{\mathrm{v}_{\mathrm{p}}}{\mathrm{v}_{\mathrm{X}}}=\dfrac{\mathrm{m}_{\mathrm{X}}}{\mathrm{m}_{\mathrm{p}}}=4$