Bán kính mặt cầu tiếp xúc với tất cả các cạnh của một hình lập phương

Bán kính mặt cầu tiếp xúc với tất cả các cạnh của một hình lập phương cạnh $\Large a$ là

• A.

  A. $\Large \dfrac{\sqrt{2a}}{2}$.

• B.

  B. $\Large \dfrac{a\sqrt{3}}{2}$.

• C.

  C. $\Large \dfrac{a}{2}$.

• D.

  D. $\Large \dfrac{a}{\sqrt{2}}$.

Chọn D

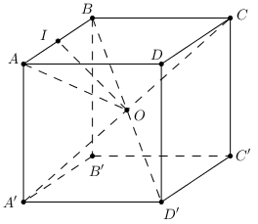
Gọi $\Large O$ là tâm hình lập phương $\Large ABCD.A'B'C'D'$ và $\Large I$ là trung điểm của $\Large AB.$

Ta có: $\Large OA=OB$ $\Large \Rightarrow \Delta OAB$ cân tại $\Large O$ $\Large \Rightarrow OI\perp AB.$

Tương tự như vậy ta chứng minh được $\Large O$ là tâm hình cầu tiếp xúc với tất cả các cạnh của hình lập phương và bán kính của hình cầu đó là $\Large R=OI.$

Ta có: $\Large A'C'=\sqrt{A'D'^2+C'D'^2}=a\sqrt{2}$

$\Large \Rightarrow AC'=\sqrt{AA'^2+A'C'^2}=a\sqrt{3}$

$\Large \Rightarrow OA=\dfrac{1}{2}AC'=\dfrac{a\sqrt{3}}{2}$

$\Large \Rightarrow OI=\sqrt{OA^2-AI^2}=\dfrac{a}{\sqrt{2}}.$