Phương trình đường tròn
Lý thuyết về Phương trình đường tròn
Phương trình đường tròn
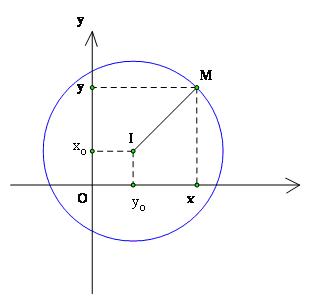
Trên mặt phẳng tọa độ, cho đường tròn (C) có tâm I(x0;y0) và bán kính R
Ta có :
Điểm M(x;y) thuộc đường tròn (C ) khi và chỉ khi IM=R, hay là
(x−x0)2+(y−y0)2=R2 (1)
Ta gọi phương trình (1) là phương trình của đường tròn (C )
Bài tập tự luyện có đáp án
Câu 1: Cho đường tròn (S):(x−2)2+(y+3)2=16 . Tìm tọa độ tâm I và bán kính R của đường tròn (S) .
- A
- B
- C
- D
Đường tròn (S):(x−2)2+(y+3)2=16 có tâm I(2;−3) , bán kính R=4 .
Câu 2: Đường tròn tâm I(−1;2) và đi qua điểm M(2;1) có phương trình là
- A
- B
- C
- D
Đường tròn có tâm I(−1;2) và đi qua M(2;1) thì có bán kính là: R=IM=√32+(−1)2=√10
Khi đó có phương trình là: (x+1)2+(y−2)2=10⇔x2+y2+2x−4y−5=0
Câu 3: Đường tròn nào sau đây đi qua điểm A(4;−2) ?
- A
- B
- C
- D
Điểm A(4;−2) thỏa mãn phương trình x2+y2−2x+6y=0. nên A∈x2+y2−2x+6y=0.
Câu 4: Trong mặt phẳng tọa độ Oxy , phương trình đường tròn có tâm I(1;4) và đi qua điểm B(2;6) là
- A
- B
- C
- D
Bán kính của đường tròn là R=IB= √(2−1)2+(6−4)2=√5 .
Phương trình đường tròn có tâm I(1;4) và đi qua điểm B(2;6) là (x−1)2+(y−4)2=5 .
Câu 5: Đường tròn x2+y2−10x−11=0 có bán kính bằng bao nhiêu?
- A
- B
- C
- D
Có a=5,b=0,c=−11 bán kính √a2+b2−c=6
Câu 6: Đường tròn tâm I(1;4) và đi qua điểm B(2;6) có phương trình là
- A
- B
- C
- D
Đường tròn có tâm I(1;4) và đi qua B(2;6) thì có bán kính là: R=IB=√(2−1)2+(6−4)2=√5
Khi đó có phương trình là: (x−1)2+(y−4)2=5
Câu 7: Đường tròn 2x2+2y2−8x+4y−1=0 có tâm là điểm nào trong các điểm sau đây ?
- A
- B
- C
- D
Ta có: 2x2+2y2−8x+4y−1=0⇔x2+y2−4x+2y−12=0 nên {−2a=−4−2b=2⇒{a=2b=−1 nên tâm I(2;−1) .
Câu 8: Đường tròn x2+y2−6x−8y=0 có bán kính bằng bao nhiêu ?
- A
- B
- C
- D
R=√a2+b2−c=√32+42−0=5