Góc tạo bởi tia tiếp tuyến và dây cung
Lý thuyết về Góc tạo bởi tia tiếp tuyến và dây cung
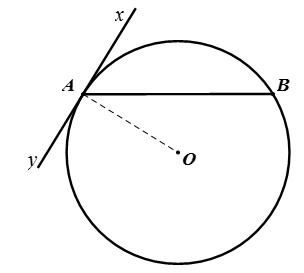
Định nghĩa: Góc $\widehat{BAx}$ có đỉnh $A$ nằm trên đường tròn, cạnh $Ax$ là một tia tiếp tuyến còn cạnh kia chứa dây cung $AB$. Ta gọi góc $\widehat{BAx}$ là góc tạo bởi tiếp tuyến và dây cung.
Định lí: Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
Hệ quả: Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác nhọn $ ABC $ $ (AB < AC) $ nội tiếp $ (O;R) $ . Gọi $ BD;CE $ là hai đường cao của tam giác. Gọi $ d $ là tiếp tuyến tại $ A $ của $ (O;R) $ và $ M,N $ lần lượt là hình chiếu của $ B,C $ trên $ d $ . Tam giác $ AMB $ đồng dạng với tam giác
- A
- B
- C
- D
Xét $ (O) $ có $ \widehat{MAB}=\widehat{ACB} $ cùng bằng một nửa sd $ \overset\frown{AB} $
Mà góc $ \widehat{AMB}=\widehat{CDB} $
$ \Rightarrow \Delta AMB $ $ \backsim $ $ \Delta CDB $ (g - g)
Câu 2: So sánh $ \widehat{APB} $ và $ \widehat{ABT} $ trong hình vẽ dưới đây biết $ BT $ là tiếp tuyến của đường tròn $ (O) $ . 
- A
- B
- C
- D
Xét đường tròn $ (O) $ có $ \widehat{ABT} $ là góc tạo bởi tiếp tuyến $ BT $ và dây cung $ AB $
$ \widehat{APB} $ là góc nội tiếp chắn cung $ AB $
Suy ra $ \widehat{ABT}=\widehat{APB} $ (hệ quả).
Câu 3: Cho đường tròn $ (O;R) $ với $ A $ là điểm cố định trên đường tròn. Kẻ tiếp tuyến $ Ax $ với $ (O) $ và lấy $ M $ là điểm bất kì thuộc tia $ Ax $ . Vẽ tiếp tuyến thứ hai $ MB $ với đường tròn $ (O) $ . Gọi $ I $ là trung điểm $ MA,K $ là giao điểm của $ BI $ với $ (O) $ . Tam giác $ IKA $ đồng dạng với tam giác
- A
- B
- C
- D
Ta có $ \widehat{IAK}=\widehat{IBA} $ bằng một nửa số đo cung $ \overset\frown{AK} $
Xét $ \Delta IKA $ và $ \Delta IAB $ có
$ \widehat{IAK}=\widehat{IBA} $
Góc $ \widehat{AIK} $ chung
Nên $ \Delta IKA $ $ \backsim $ $ \Delta IAB $ (g – g)
Câu 4: Cho nửa đường tròn tâm $ O $ bán kính $ R $ đường kính $ AB $ . Trên nửa đường tròn lấy điểm $ M $ sao cho $ AM=R\sqrt{3} $ . $ AM $ cắt tiếp tuyến tại $ B $ của đường tròn tại $ N $ . Số đo góc $ \widehat{MBN} $ là :
- A
- B
- C
- D
Tam giác $ AMB $ có $ \cos \widehat{MAB}=\dfrac{AM}{AB}=\dfrac{\sqrt{3}}{2}\Rightarrow \widehat{MAB}={{30}^{{}^\circ }} $ .
Câu 5: Chọn câu sai khi nói về góc tạo bởi tiếp tuyến và dây cung :
- A
- B
- C
- D
Câu 6: Cho đường tròn $ (O;R) $ có hai đường kính $ AB $ và $ CD $ vuông góc. Gọi $ I $ là điểm trên cung $ AC $ sao cho khi vẽ tiếp tuyến qua $ I $ và cắt $ DC $ kéo dài tại $ M $ thì $ \widehat{CIM}=30{}^\circ $ . Số đo góc $ AOI $ là
- A
- B
- C
- D
Ta có: $ \widehat{CIM} $ là góc tạo bởi tiếp tuyến và dây cung chắn cung $ \overset\frown{IC} $
$ \widehat{IOC} $ là góc ở tâm chắn cung $ \overset\frown{IC} $
$ \Rightarrow \widehat{CIM}=\dfrac{1}{2}\widehat{IOC}\Rightarrow \widehat{IOC}=2\widehat{CIM}=2.30{}^\circ =60{}^\circ $
$ \Rightarrow \widehat{IOA}=90{}^\circ -60{}^\circ =30{}^\circ $ .
Câu 7: Cho tam giác $ ABC $ nội tiếp đường tròn $ (O) $ , tiếp tuyến tại $ A $ của $ (O) $ cắt $ BC $ tại $ P $ . Hai tam giác đồng dạng là
Hai tam giác đồng dạng là
- A
- B
- C
- D
Xét $ (O) $ có $ \widehat{ACB}=\widehat{BAP} $ đều bằng một nửa số đo cung $ \overset\frown{AB} $
Xét tam giác $ \Delta PAC $ và $ \Delta PBA $ có
$ \widehat{ACB}=\widehat{BAP} $
Góc $ \widehat{P} $ chung
Suy ra $ \Delta PAC $ $ \backsim $ $ \Delta PBA $ (g - g)
Câu 8: Kết luận nào sau đây là đúng.
- A
- B
- C
- D
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Xem thêm các bài tiếp theo bên dưới