Hình hộp chữ nhật
Lý thuyết về Hình hộp chữ nhật
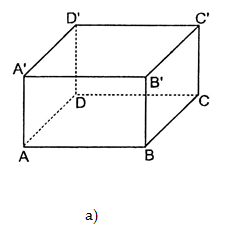
1. Định nghĩa: Hình hộp chữ nhật có 6 mặt là hình chữ nhật (hình a). Hình lập phương là hình hộp chữ nhật có $6$ mặt là hình vuông (hình b).
Bài tập tự luyện có đáp án
Câu 1: Khẳng định đúng là
- A
- B
- C
- D

+) Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau là SAI. Chẳng hạn $ AB $ và $ AB' $ đều song song với mặt phẳng $ \left( CC'D'D \right) $ nhưng chúng lại không song song với nhau.
+) Hai đường thẳng phân biệt cùng song song với 1 đường thẳng thì song song với nhau.ĐÚNG
+) Hai mặt phẳng phân biệt cùng song song với 1 đường thẳng thì song song với nhau. SAI . Chẳng hạn 2 mặt phẳng $ \left( AA'B'B \right) $ và $ \left( BB'C'C \right) $ cùng song song với đường thẳng $ DD' $ nhưng 2 mặt phẳng này ko song song với nhau.
+) Mặt phẳng $ \left( \alpha \right) $ song song với đường thẳng $ d $ thì $ \left( \alpha \right) $ sẽ song song với mặt phẳng $ \left( \beta \right) $ chứa $ d $ . SAI vì $ \left( \alpha \right)//\left( \beta \right) $ khi và chỉ khi $ \left( \alpha \right) $ phải song song với 2 đường thẳng cắt nhau nằm trong $ \left( \beta \right) $ .
Câu 2: Cho hình lăng hộp chữ nhật $ ABCD.A'B'C'D' $ . Khẳng định sai trong các khẳng định sau là
- A
- B
- C
- D

$ AB//CD\Rightarrow AB//\left( CDD'C' \right) $ (đúng)
Ta có $ AA' $ và $ AD $ cắt nhau, $ BB' $ và $ BC $ cắt nhau đòng thời $ \left\{ \begin{array}{l} AA'//BB' \\ AD//BC \end{array} \right.\Rightarrow \left( AA'D'D \right)//\left( BB'C'C \right) $ (đúng)
$ AC//A'C'\Rightarrow AC//\left( A'B'C'D' \right) $ (đúng)
$ C'D//\left( BB'D'D \right) $ sai vì $ C'D\cap \left( BB'D'D \right)=\left\{ D \right\} $
Câu 3: Cho hình hộp chữ nhật $ ABCD.A'B'C'D' $ . $ M,N,I,K $ lần lượt là trung điểm của $ AD,DC,A'B',B'C' $ . Tứ giác $ MNKI $ là hình gì?
- A
- B
- C
- D

M là trung điểm AD, N là trung điểm DC suy ra MN là đường trung bình của tam giác ADC, suy ra $ \left\{ \begin{array}{l} MN//AC \\ MN=\dfrac{1}{2}AC \end{array} \right. $
Chứng minh tương tự ta có $ \left\{ \begin{array}{l} IK//A'C' \\ IK=\dfrac{1}{2}A'C' \end{array} \right. $
Mà $ \left\{ \begin{array}{l} A'C'//AC \\ A'C'=AC \end{array} \right. $ $ \Rightarrow \left\{ \begin{array}{l} IK//MN \\ IK=MN \end{array} \right. $ . Vậy tứ giác $ MNKI $ là hình bình hành.
Câu 4: Cho hình hộp chữ nhật $ ABCD.A'B'C'D' $ .M, N lần lượt là trung điểm $ A'B' $ và $ A'D' $ . Khẳng định nào sai trong các khẳng định sau?
- A
- B
- C
- D

MN là đường trung bình của tam giác $ A'B'D' $ suy ra $ MN//B'D'\Rightarrow MN//BD $
$ \Rightarrow $ $ MN//\left( BB'D'D \right) $ , $ MN//\left( C'BD \right) $ $ MN//\left( CB'D' \right) $
$ MN//\left( BB'C' \right) $ là sai.
Câu 5: Cho hình lập phương $ ABCD.A'B'C'D' $ . Cặp đường thẳng nào sau đây không cùng thuộc một mặt phẳng?
- A
- B
- C
- D

$ AC//A'C' $ nên $ AC $ và $ A'C' $ đồng phẳng.
$ A'B//CD' $ nên $ A'B $ và $ CD' $ đồng phẳng.
$ B'C//DA' $ nên $ B'C $ và $ DA' $ đồng phẳng.
Câu 6: Cho hình hộp chữ nhật $ ABCD.MNPQ $ . O là trung điểm AN. Biết $ OA=3 $ , $ PQ=4 $ . Diện tích $ ABNM $ bằng
- A
- B
- C
- D

$ ABNM $ là hình chữ nhật.
$ OA=3\Rightarrow AN=6 $
$ AB=PQ=4 $
$ NB=\sqrt{A{{N}^{2}}-A{{B}^{2}}}=\sqrt{{{6}^{2}}-{{4}^{2}}}=2\sqrt{5} $ .
Diện tích ABNM: $ S=AB.NB=4.2\sqrt{5}=8\sqrt{5} $
Câu 7: Cho các khẳng định về hình hộp chữ nhật như sau: (I) Các cạnh bên luôn song song với nhau.
(II) Các cạnh bên đều vuông góc với hai mặt đáy.
(III) Hình hộp chữ nhật có hai đường chéo.
(IV) Các cạnh đáy song song với nhau.
Có bao nhiêu khẳng định đúng trong các khẳng định trên.
(I) Các cạnh bên luôn song song với nhau.
(II) Các cạnh bên đều vuông góc với hai mặt đáy.
(III) Hình hộp chữ nhật có hai đường chéo.
(IV) Các cạnh đáy song song với nhau.
Có bao nhiêu khẳng định đúng trong các khẳng định trên.
- A
- B
- C
- D
Trong hình hộp chữ nhật ác cạnh bên luôn song song với nhau, các cạnh bên đều vuông góc với hai mặt đáy và hình hộp chữ nhật có hai đường chéo chính.
Câu 8: Trong các mặt phẳng của một hình hộp chữ nhật, tính số cặp mặt song song với nhau là
- A
- B
- C
- D
Có $ 3 $ cặp mặt phẳng song song là mp $ (AB{B}'{A}') $ và mp $ (DC{C}'{D}') $ ; mp $ (ABCD) $ và mp $ ({A}'{B}'{C}'{D}') $ ; mp $ (AD{D}'{A}') $ và mp $ (BC{C}'{B}') $ .
Câu 9: Hãy chọn câu sai. Hình hộp chữ nhật $ ABCD.{A}'{B}'{C}'{D}' $ có.
- A
- B
- C
- D
Hình hộp chữ nhật có $ 12 $ cạnh:
$ \begin{array}{*{35}{l}} AB;BC;CD;DA;{A}'{B}';{C}'{D}'; \\ {B}'{C}';{D}'{A}';A{A}';B{B}';C{C}';D{D}'. \end{array} $
Câu 10: Cho hình hộp chữ nhật $ ABCD.{A}'{B}'{C}'{D}' $ . Hãy chọn khẳng định sai.
- A
- B
- C
- D
Các cạnh bằng nhau của hình hộp chữ nhật
$ \begin{array}{l} AB=DC={A}'{B}'={D}'{C}' \\ A{A}'=B{B}'=C{C}'=D{D}' \\ A{A}'=B{B}'=C{C}'=D{D}'. \end{array} $
Câu 11: Cho hình hộp chữ nhật $ ABCD.{A}'{B}'{C}'{D}' $ . Có bao nhiêu cạnh cắt cạnh $ AB $ .
- A
- B
- C
- D
Có bốn cạnh cắt $ AB $ là $ AD,AA\prime ,BC,BB\prime $ .
Câu 12: Hình hộp chữ nhật có bao nhiêu mặt?
- A
- B
- C
- D

Hình hộp chữ nhật có 6 mặt.
Câu 13: Cho hình hộp chữ nhật $ ABCD.{A}'{B}'{C}'{D}' $ . Chọn khẳng định đúng.
- A
- B
- C
- D
Ta có $ A{C}' $ cắt $ D{B}' $ vì $ AD\text{//}{B}'{C}';AD={B}'{C}' $ nên $ AD{C}'{B}' $ là hình bình hành, do đó $ A{C}' $ cắt $ D{B}' $ .
$ A{C}' $ không cắt $ BC $ vì chúng không có điểm chung.
$ AB $ và $ CD $ song song nên chúng không cắt nhau.
$ AC~ $ và $ BD $ cắt nhau.
Câu 14: Cho hình hộp chữ nhật $ ABCD.MNPQ $ . O là trung điểm AN, K thuộc MQ sao cho $ KQ=\dfrac{2}{5}MQ $ . Khẳng định nào sau đây đúng?
- A
- B
- C
- D

ABNM là hình chữ nhật, mà O là trung điểm AN nên O cũng là trung điểm MB, hay M,O,B thẳng hàng.
Câu 15: Hình hộp chữ nhật $ ABCD.{A}'{B}'{C}'{D}' $ . Gọi tên mặt phẳng chứa đường thẳng $ {A}'B $ và $ C{D}' $ . Hãy chọn đáp án đúng.
- A
- B
- C
- D
Mặt phẳng chứa đường thẳng $ {A}'B $ và $ C{D}' $ là mặt phẳng đi qua bốn
điểm $ {A}',B,C,{D}' $ hay chính là $ mp(A\prime BCD\prime ). $
Câu 16: Hình hộp chữ nhật có tất cả các mặt là hình
- A
- B
- C
- D
Các mặt của hình hộp chữ nhật đều là hình chữ nhật.
Câu 17: Đâu không phải là một mặt của hình chữ nhật $ ABCD.{A}'{B}'{C}'{D}' $ .
- A
- B
- C
- D
Hình hộp chữ nhật gồm $ 6 $ mặt:
$ (AD{D}'{A}');(DC{C}'{D}');(BC{C}'{B}');(AB{B}'{A}');(ABCD);({A}'{B}'{C}'{D}') $ .
Câu 18: Hình hộp chữ nhật có bao nhiêu cạnh?
- A
- B
- C
- D

Hình hộp chữ nhật có 12 cạnh.
Câu 19: Các mặt của hình hộp chữ nhật là hình gì:
- A
- B
- C
- D
Các mặt của hình hộp chữ nhật đều là hình chữ nhật.
Câu 20: Hình hộp chữ nhật có bao nhiêu đỉnh?
- A
- B
- C
- D
Hình hộp chữ nhật có 8 đỉnh.
Câu 21: Khẳng định nào đúng khi nói về hình lập phương
- A
- B
- C
- D
Hình hộp chữ nhật có các mặt bên là hình vuông thì khi đó, tất cả các cạnh đều bằng nhau, hay trở thành hình lập phương.
Câu 22: Cho hình hộp chữ nhật $ ABCD.{A}'{B}'{C}'{D}' $ . Có bao nhiêu cạnh song song với cạnh $ AB $ .
- A
- B
- C
- D
Có ba cạnh song song với $ AB $ là $ {A}'{B}',CD,{C}'{D}' $ .
Câu 23: Một hình hộp chữ nhật có các độ dài là $ 3cm,4cm,5cm $ thì có thể tích bằng?
- A
- B
- C
- D
$ V=3.4.5=60\left( c{{m}^{3}} \right) $
Câu 24: Hãy chọn đáp án đúng. Cạnh của một hình lập phương bằng $ 5cm $ khi đó thể tích của nó là
- A
- B
- C
- D
Thể tích hình lập phương cạnh $ 5c{{m}^{3}} $ là: $ V={{5}^{3}}=125\,c{{m}^{3}} $ .
Câu 25: Cho hình hộp chữ nhật $ ABCD.{A}'{B}'{C}'{D}' $ . Đường thẳng $ B{B}' $ vuông góc với các mặt phẳng nào?
- A
- B
- C
- D
Ta có:
$ B{B}'\bot BC $ (Vì $ BC{C}'{B}' $ là hình chữ nhật)
$ B{B}'\bot BA $ (Vì $ AB{B}'{A}' $ là hình chữ nhật)
$ \Rightarrow B{B}'\bot mp(ABCD) $
Ta có:
$ B{B}'\bot {B}'{C}' $ (Vì $ BC{C}'{B}' $ là hình chữ nhật)
$ B{B}'\bot {B}'{A}' $ (Vì $ AB{B}'{A}' $ là hình chữ nhật)
$ \Rightarrow B{B}'\bot mp({A}'{B}'{C}'{D}') $
Vậy $ B{B}' $ vuông góc với mặt phẳng $ (ABCD) $ và mặt phẳng $ {A}'{B}'{C}'{D}' $ .
Câu 26: Cho hình lập phương $ ABCD.A'B'C'D' $ . Khẳng định nào sau đây sai?
- A
- B
- C
- D

$ \left\{ \begin{array}{l} BC\bot AB \\ BC\bot BB' \end{array} \right.\Rightarrow BC\bot \left( ABB'A' \right)\Rightarrow \left( ABCD \right)\bot \left( AA'B'B \right) $
$ \left\{ \begin{array}{l} BC\bot CD \\ BC\bot CC' \end{array} \right.\Rightarrow BC\bot \left( CC'D'D \right)\Rightarrow \left( BB'C'C \right)\bot \left( CC'D'D \right) $
$ ABCD $ là hình vuông nên $ BD\bot AC $ . Mà $ BB'\bot \left( ABCD \right)\Rightarrow BB'\bot AC $
Suy ra $ \left\{ \begin{array}{l} AC\bot BD \\ AC\bot BB' \end{array} \right.\Rightarrow AC\bot \left( BB'D'D \right)\Rightarrow \left( ACC'A' \right)\bot \left( BB'D'D \right) $
Câu 27: Hình lập phương cạnh bằng $ 4\left( cm \right) $ thì có thể tích bằng
- A
- B
- C
- D
$ V={{a}^{3}}={{4}^{3}}=64\left( c{{m}^{3}} \right) $
Câu 28: Cho hình hộp chữ nhật $ ABCD.A'B'C'D' $ . Khẳng định nào sau đây sai?
- A
- B
- C
- D

$ \left\{ \begin{array}{l} AB\bot \left( AA' \right) \\ AB\bot \left( AD \right) \end{array} \right.\Rightarrow AB\bot \left( AA'D'D \right) $
$ \left\{ \begin{array}{l} BC\bot AB \\ BC\bot BB' \end{array} \right.\Rightarrow BC\bot \left( ABB'A' \right) $
$ \left\{ \begin{array}{l} AA'\bot AB \\ AA'\bot AD \end{array} \right.\Rightarrow AA'\bot \left( ABCD \right) $
$ AC $ không vuông góc với $ BD $ nên $ AC $ không vuông góc với $ \left( BB'D'D \right) $