Góc nội tiếp
Lý thuyết về Góc nội tiếp
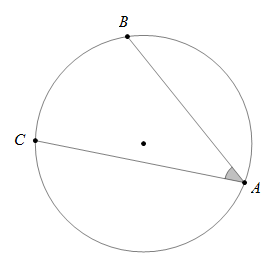
Định nghĩa: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh cắt đường tròn đó.
Cung nằm bên trong góc là cung bị chắn.
Trong đường tròn tâm OO ta có góc ^BACˆBAC là góc nội tiếp, cung bị chắn là cung ⌢BC⌢BC.
Định lí: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
^BAC=12ˆBAC=12 ⌢BC⌢BC
Hệ quả: Trong một đường tròn:
- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
- Các góc nội tiếp chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
- Góc nội tiếp ( nhỏ hơn hoặc bằng 90∘90∘ ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
- Góc nội tiếp chắn nửa đường tròn là góc vuông
Bài tập tự luyện có đáp án
Câu 1: Góc nội tiếp chắn nửa đường tròn bằng
- A
- B
- C
- D
Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
Câu 2: Cho tam giác ΔABCΔABC có ˆA=40∘ˆA=40∘, ˆB=60∘ˆB=60∘, ˆC=80∘ˆC=80∘. OO là giao điểm của ba đường trung trực của các cạnh AB,BC,CAAB,BC,CA. Số đo góc ^COAˆCOA bằng bao nhiêu?
- A
- B
- C
- D
Ta có tam giác ABCABC khi đó nội tiếp đường tròn (O)(O), góc ^CBAˆCBA khi đó là góc nội tiếp chắn cung⌢AC⌢AC nên ^COA=2^CBA=120∘ˆCOA=2ˆCBA=120∘.
Câu 3: Cho đường tròn tâm OO bán kính RR , dây cung AB=R√2AB=R√2. Gọi CC là điểm bất kì trên cung lớn ABAB. Tính số đo góc ^ACBˆACB.
- A
- B
- C
- D
Do OA2+OB2=AB2OA2+OB2=AB2 nên ΔAOBΔAOB vuông tại O
Suy ra ^ACB=12^AOB=1290∘=45∘ˆACB=12ˆAOB=1290∘=45∘
Câu 4: Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
Trong một đường tròn
1. Các góc nội tiếp chắn cùng một cung thì bằng nhau.
2. Các góc nội tiếp bằng nhau thì chắn cùng một cung.
3. Các góc nội tiếp chắc các cung bằng nhau thì chưa chắc đã bằng nhau.
- A
- B
- C
- D
- Các góc nội tiếp bằng nhau thì có thể chắn cùng một cung hoặc chắn các cung bằng nhau.
- Các góc nội tiếp bằng nhau thì chắn các cung bằng nhau.
Câu 5: Cho (O)(O) , đường kính ABAB , điểm DD thuộc đường tròn. Gọi EE là điểm đối xứng với AA qua DD . Tam giác ABEABE là tam giác
- A
- B
- C
- D
Xét (O)(O) có ^BDA=90∘ˆBDA=90∘ (góc nội tiếp chắn nửa đường tròn) nên
BD⊥EABD⊥EA mà DD là trung điểm EAEA .
Nên ΔBEAΔBEA có BDBD vừa là đường cao vừa là đường trung tuyến
nên ΔBEAΔBEA cân tại BB .
Câu 6: Cho (O)(O) , đường kính ABAB , điểm DD thuộc đường tròn sao cho ^DAB=50∘ˆDAB=50∘ . Gọi EE là điểm đối xứng với AA qua DD . Góc ^AEBˆAEB có số đo bằng
- A
- B
- C
- D
Xét (O)(O) có ^BDA=90∘ˆBDA=90∘ (góc nội tiếp chắn nửa đường tròn) nên BD⊥EABD⊥EA mà DD là trung điểm EAEA .
Nên ΔBEAΔBEA có BDBD vừa là đường cao vừa là đường trung tuyến nên ΔBEAΔBEA cân tại BB .
Suy ra ^BEA=^BAD=50∘ˆBEA=ˆBAD=50∘ .
Câu 7: Chọn đáp án sai.
Trong một đường tròn
- A
- B
- C
- D
Trong một đường tròn góc nội tiếp có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.