Góc có đỉnh ở bên trong đường tròn, bên ngoài đường tròn
Lý thuyết về Góc có đỉnh ở bên trong đường tròn, bên ngoài đường tròn
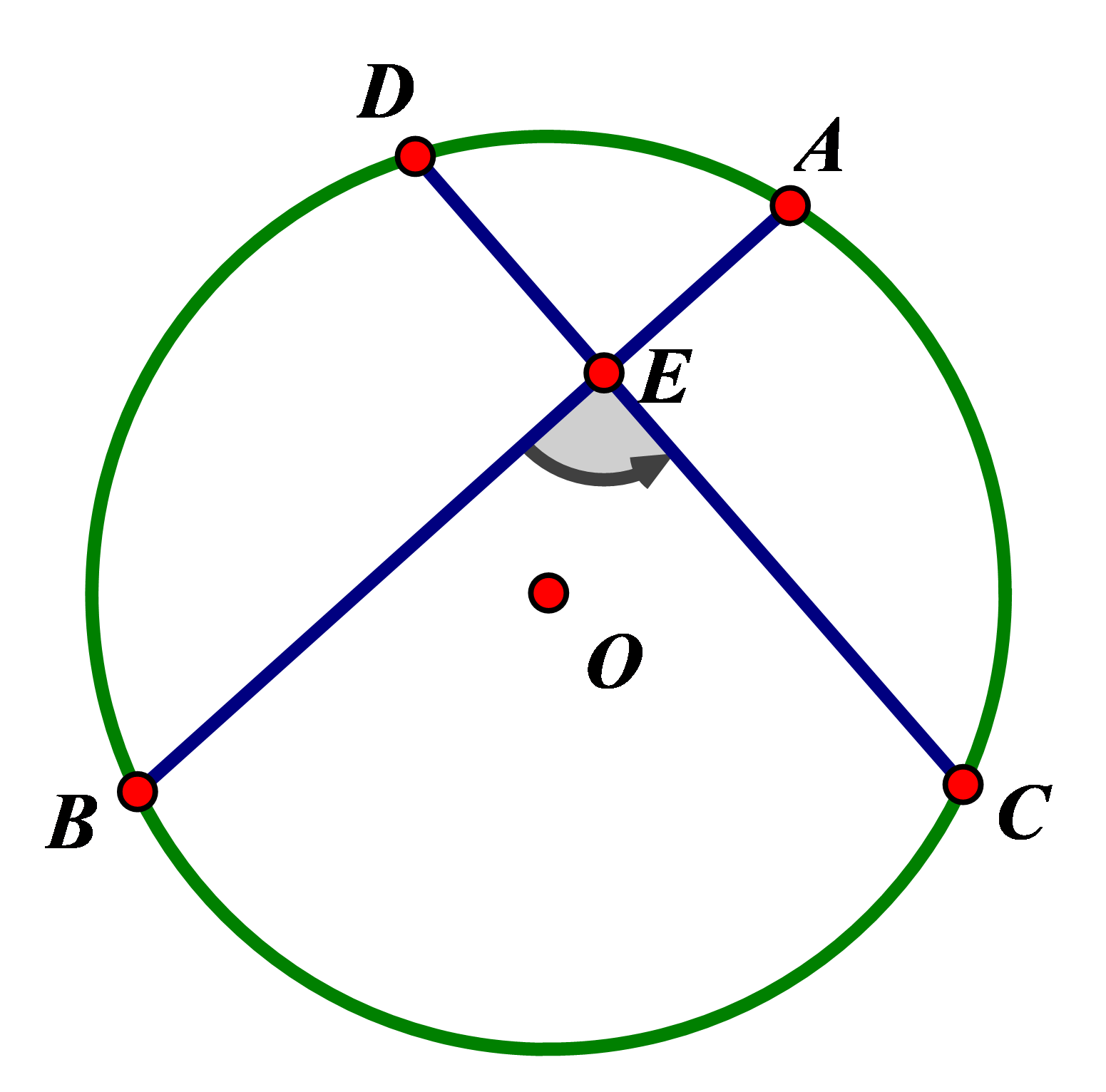
1. Góc có đỉnh ở bên trong đường tròn
Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
\[\widehat {BEC} = \dfrac{1}{2}\left( {sdAD + sdAD} \right)\]
2. Góc có đỉnh ở bên ngoài đường tròn
Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
\[\begin{array}{*{20}{l}}
{\widehat {BEC} = \dfrac{1}{2}\left( {sdBC - sdAD} \right)} \\
{\widehat {AEC} = \dfrac{1}{2}\left( {sdAmC - sdAnC} \right)}
\end{array}\]
Bài tập tự luyện có đáp án
Câu 1: Góc có đỉnh bên ngoài đường tròn có số đo
- A
- B
- C
- D
Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Câu 2: Cho hình vẽ dưới đây, góc $ DIE $ có số đo bằng:


- A
- B
- C
- D
Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
$ \widehat{DIE}= $ $ \dfrac{1}{2} $ (số đo cung $ DmE+ $ số đo cung $ CnF $ ).
Câu 3: Cho hình vẽ dưới đây, góc $ \widehat{DIE} $ có số đo bằng 
- A
- B
- C
- D
Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
$ \widehat{DIE}=\dfrac{1}{2}(\text{s}\mathrm{}\overset\frown{DmE}+\text{s}\mathrm{}\overset\frown{CnF}) $ .
Câu 4: Cho hình vẽ dưới đây, góc $ \widehat{BIC} $ có số đo bằng 
- A
- B
- C
- D
Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn:
$ \widehat{BIC}=\dfrac{1}{2}(\text{s}\mathrm{}\overset\frown{BC}-\text{s}\mathrm{}\overset\frown{AD}) $ .
Câu 5: Từ một điểm $ M $ nằm ngoài đường tròn $ \left( O \right), $ vẽ $ 2 $ cát tuyến $ MAB $ và $ MCD $ ( $ A $ nằm giữa $ M $ và $ B, $
$ C $ nằm giữa $ M $ và $ D $ ). Cho biết số đo cung nhỏ $ AC $ bằng $ {{30}^{0}} $ và số đo cung nhỏ $ BD $ bằng $ {{80}^{0}}. $ Vậy số đo góc $ M $ là:
- A
- B
- C
- D

Ta có $ \widehat{BMD} $ là góc có đỉnh nằm ngoài đường tròn nên
$ \widehat{BMD}=\dfrac{1}{2} $ (sđ $ \overset\frown{BD}- $ sđ $ \overset\frown{AC} $ ) $ =\dfrac{1}{2}\left( {{80}^{0}}-{{30}^{0}} \right)={{25}^{0}} $ .
Câu 6: Cho hình vẽ dưới đây, góc $ BIC $ có số đo bằng:


- A
- B
- C
- D
Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
$ \widehat{BIC}= $ $ \dfrac{1}{2} $ (số đo cung nhỏ $ BC- $ số đo cung nhỏ $ AD $ ).
Câu 7: Góc có đỉnh bên trong đường tròn có số đo
- A
- B
- C
- D
Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.