Mạch xoay chiều chỉ chứa R.

Điện trở thuần biến toàn bộ điện năng qua nó thành nhiệt.

Đặt vào 2 đầu 1 điện áp xoay chiều: $u={{U}_{0}}cos(\omega t+\varphi )$

Xét $\Delta t$ vô cùng nhỏ thì dòng xoay chiều như dòng 1 chiều. Theo định luật Ôm.

$i=\dfrac{u}{R}\Rightarrow i=\dfrac{{{U}_{0}}}{R}\cos \left( \omega t+\varphi  \right)={{I}_{0}}\cos \left( \omega t+\varphi  \right)$ với ${{I}_{0}}=\dfrac{{{U}_{0}}}{R}$

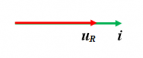
Trong mạch chỉ chứa R: u và i cùng pha.

Chú ý: công thức tính điện trở dây dẫn: $R=\rho \dfrac{\ell }{S}$

Trong đó: 

R là điện trở dây dẫn $\left( \Omega  \right)$

$\rho$ là điện trở suất của dây dẫn $\left( \Omega .m \right)$

$\ell$ là chiều dài dây dẫn (m)

S là tiết diện của dây dẫn $\left( {{m}^{2}} \right)$