Tỉ số lượng giác của góc nhọn
Lý thuyết về Tỉ số lượng giác của góc nhọn
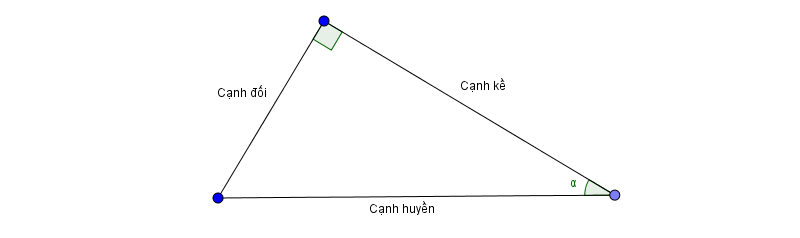
Khái niệm tỉ số lượng giác của một góc nhọn.
Từ định nghĩa trên, dễ thấy các tỉ số lượng giác của một góc nhọn luôn luôn dương. Hơn nữa ta có: $\sin{\alpha} < 1, \cos{\alpha} < 1$.
Tỉ số lượng giác của hai góc phụ nhau.
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
$\sin{\alpha} = \cos{\beta}, \cos{\alpha} = \sin{\beta}, \tan{\alpha} = \cot{\beta}, \cot{\alpha} = \tan{\beta}$.
Với mọi góc nhọn $\alpha $ ta có $0<\sin \alpha <1,0<\cos \alpha <1$
\[{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\]
\[tag\alpha =\dfrac{\sin \alpha }{\cos \alpha }\]
\[\cot \alpha =\dfrac{\cos \alpha }{\sin \alpha }\]
\[tag\alpha .\cot \alpha =1\]
Bài tập tự luyện có đáp án
Câu 1: Cho một tam giác vuông, có góc nhọn $a$. Câu nào sau đây sai?
- A
- B
- C
- D
Câu 2: Trong hình vẽ bên, $ \sin Q $ bằng:


- A
- B
- C
- D
Theo định nghĩa: $ \sin Q=\dfrac{PR}{PQ} $ .
Câu 3: Cho tam giác $ ABC $ vuông tại $ A $ có $ BC=8\,cm,AC=6\,cm $ . Tính tỉ số lượng giác $ \tan C $ (làm tròn đến chữ số thập phân thứ 2).
- A
- B
- C
- D
Theo định lý Pytago ta có: $ B{{C}^{2}}=A{{C}^{2}}+A{{B}^{2}}\Rightarrow AB=\sqrt{{{8}^{2}}-{{6}^{2}}}\approx 5,29 $ .
Xét tam giác $ ABC $ vuông tại $ C $ có $ \tan C=\dfrac{AB}{AC}\approx \dfrac{5,29}{6}\approx 0,88 $ .
Câu 4: Với góc nhọn $ \beta $ tùy ý, khẳng định nào sau đây sai ?
- A
- B
- C
- D
Có công thức $ \cot \beta =\dfrac{\text{cos}\beta }{\sin \beta } $ nên khẳng định $ \cot \beta =\dfrac{\sin \beta }{\text{cos}\beta } $ sai.
Câu 5: Cho tam giác $ MNP $ vuông tại $ P $ , trong đó $ MP=4,5 $ , $ NP=6 $ . Tính các tỉ số lượng giác của góc $ N $ .
- A
- B
- C
- D
$ MN=\sqrt{{{4,5}^{2}}+{{6}^{2}}}=\sqrt{20,25+36}=\sqrt{56,25}=7,5 $ .
$ \sin N=\dfrac{MP}{NM}=\dfrac{45}{75}=\dfrac{3}{5} $ .
$ \cos N=\sqrt{1-{{\sin }^{2}}N}=\sqrt{1-\dfrac{9}{25}}=\dfrac{4}{5} $ .
$ \tan N=\dfrac{\sin N}{\cos N}=\dfrac{3}{4} $ .
$ \cot N=\dfrac{1}{\tan N}\text{=}\dfrac{4}{3} $ .
Câu 6: Tính $ \sin \alpha ,\tan \alpha $ biết $ \cos \alpha =\dfrac{3}{4} $ .
- A
- B
- C
- D
Ta có $ {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\Rightarrow {{\sin }^{2}}\alpha =1-{{\cos }^{2}}\alpha =1-\dfrac{9}{16}=\dfrac{7}{16} $ .
$ \Rightarrow \sin \alpha =\dfrac{\sqrt{7}}{4} $ .
Lại có $ \tan \alpha =\dfrac{\sin \alpha }{\cos \alpha }=\dfrac{\dfrac{\sqrt{7}}{4}}{\dfrac{3}{4}}=\dfrac{\sqrt{7}}{3} $ .
Vậy $ \sin \alpha =\dfrac{\sqrt{7}}{4};\tan \alpha =\dfrac{\sqrt{7}}{3} $ .
Câu 7: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ có $ CH=4cm,BH=3cm $ . Tính tỉ số lượng giác $ \cos C $ (làm tròn đến chữ số thập phân thứ 2).
- A
- B
- C
- D
Xét tam giác $ ABC $ vuông tại $ A $ có $ BC=BH+CH=7cm $
Theo hệ thức lượng trong tam giác vuông ta có
$ A{{C}^{2}}=CH.BC\Rightarrow A{{C}^{2}}=4.7\Rightarrow AC\approx 5,29cm\Rightarrow \cos C=\dfrac{AC}{BC}=\dfrac{5,29}{7}\approx 0,76 $ .
Câu 8: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ có $ CH=11cm,BH=12cm $ . Tính tỉ số lượng giác $ \cos C $ (làm tròn đến chữ số thập phân thứ 2).
- A
- B
- C
- D
Xét tam giác $ ABC $ vuông tại $ A $ có $ BC=BH+CH=11+12=23cm $ .
Theo hệ thức lượng trong tam giác vuông ta có:
$ A{{C}^{2}}=CH.BC\Rightarrow A{{C}^{2}}=11.23=253\Rightarrow AC=\sqrt{253}cm $
$ \Rightarrow \cos C=\dfrac{AC}{BC}=\dfrac{\sqrt{253}}{23}\approx 0,69 $ .
Câu 9: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ có $ AB=13cm,BH=0,5dm $ . Tính tỉ số lượng giác $ \sin C $ (làm tròn đến chữ số thập phân thứ 2)
- A
- B
- C
- D
Đổi $ 0,5dm=5cm $
Xét tam giác $ ABC $ vuông tại $ A $ , theo hệ thức lượng
trong tam giác vuông ta có:
$ A{{B}^{2}}=BH.BC\Rightarrow BC=\dfrac{A{{B}^{2}}}{BH}=\dfrac{{{13}^{2}}}{5}=33,8cm $
$ \Rightarrow \sin C=\dfrac{AB}{BC}=\dfrac{13}{33,8}\approx 0,38 $
Câu 10: Cho tam giác $ ABC $ vuông tại $ A $ . Hãy tính $ \tan C $ biết rằng $ \tan B=4 $ .
- A
- B
- C
- D
Vì tam giác $ ABC $ vuông tại $ A $ nên $ \widehat{B}+\widehat{C}=90{}^\circ \Rightarrow \cot C=\tan B=4 $
Mà $ \cot C.\tan C=1\Rightarrow \tan C=\dfrac{1}{4} $ .
Câu 11: Cho tam giác vuông $ ABC $ vuông tại $ A $ , độ dài cạnh $ AB=2 $ và $ AC=5 $ . Tính giá trị $ \sin $ của góc $ ABC. $
- A
- B
- C
- D
Tam giác vuông $ ABC $ vuông tại $ A $ , nên $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}=29\Rightarrow BC=\sqrt{29} $ .
Trong tam giác $ ABC $ ta có $ \sin \widehat{ACB}=\dfrac{AB}{BC}=\dfrac{2}{\sqrt{29}}=\dfrac{2\sqrt{29}}{29} $ .
Câu 12: Cho tam giác $ ABC $ vuông tại $ A $ có $ BC=9cm,AC=5cm $ . Tính tỉ số lượng giác $ \tan C $ (làm tròn đến chữ số thập phân thứ 1)
- A
- B
- C
- D
Theo định lý Pytago ta có: $ B{{C}^{2}}=A{{C}^{2}}+A{{B}^{2}}\Rightarrow AB=\sqrt{{{9}^{2}}-{{5}^{2}}}=2\sqrt{14} $ .
Xét tam giác $ ABC $ vuông tại $ C $ có $ \tan C=\dfrac{AB}{AC}=\dfrac{2\sqrt{14}}{5}\approx 1,5 $ .
Câu 13: Cho tam giác $ ABC $ vuông tại $ C $ có $ BC=1,2cm,AC=0,9cm $ . Tính các tỉ số lượng giác $ \sin B;\cos B $ .
- A
- B
- C
- D
Theo định lý Pytago ta có
$ A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}\Rightarrow AB=\sqrt{0,{{9}^{2}}+1,{{2}^{2}}}=1,5 $
Xét tam giác $ ABC $ vuông tại $ C $ có $ \sin B=\dfrac{AC}{AB}=\dfrac{0,9}{1,5}=\dfrac{3}{5}=0,6 $ và $ \cos B=\dfrac{BC}{AB}=\dfrac{1,2}{1,5}=\dfrac{4}{5}=0,8 $ .
Câu 14: Cho tam giác $ ABC $ vuông tại $ A $ có $ AB=9\,cm,\tan C=\dfrac{5}{4} $ . Tính độ dài các đoạn thẳng $ AC $ và $ BC $ . (làm tròn đến chữ số thập phân thứ 2).
- A
- B
- C
- D
Vì tam giác $ ABC $ vuông tại $ A $ nên $ \tan C=\dfrac{AB}{AC}\Rightarrow AC=AB:\tan C=9:\dfrac{5}{4}=7,2\,cm $
Theo định lý Pytago ta có $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}={{9}^{2}}+7,{{2}^{2}}=132,84\Rightarrow BC=\dfrac{9\sqrt{41}}{5}\approx 11,53 $ .
Vậy $ AC=7,2;BC\approx 11,53 $ .
Câu 15: Cho tam giác $ ABC $ vuông tại $ A $ có $ AB=5cm,\cot C=\dfrac{7}{8} $ . Tính độ dài các đoạn thẳng $ AC $ và $ BC $ (làm tròn đến chữ số thập phân thứ 2)
- A
- B
- C
- D
Vì tam giác $ ABC $ vuông tại $ A $ nên $ \cot C=\dfrac{AC}{AB}\Rightarrow AC=AB.\cot C=5.\dfrac{7}{8}=\dfrac{35}{8}\approx 4,38\,cm $ .
Theo định lý Pytago ta có $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}={{5}^{2}}+4,{{38}^{2}}\Rightarrow BC\approx 6,65 $ .
Vậy $ AC\approx 4,38(cm);BC\approx 6,65\,(cm) $ .
Câu 16: Cho tam giác $ ABC $ vuông tại $ C $ có $ AC=1cm,BC=2cm $ . Tính các tỉ số lượng giác $ \sin B;\cos B $ lần lượt là
- A
- B
- C
- D
Theo định lý Pytago ta có $ A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}\Rightarrow AB=\sqrt{{{1}^{2}}+{{2}^{2}}}=\sqrt{5} $ .
Xét tam giác $ ABC $ vuông tại $ C $ có $ \sin B=\dfrac{AC}{AB}=\dfrac{1}{\sqrt{5}}=\dfrac{\sqrt{5}}{5} $ và $ \cos B=\dfrac{BC}{AB}=\dfrac{2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{5} $ .
Câu 17: Cho góc nhọn $ \alpha $ . Nếu $ \sin \alpha =\dfrac{3}{5} $ , thì $ \cos \alpha $ bằng
- A
- B
- C
- D
Áp dụng công thức
$ \begin{array}{l}
& {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1 \\
& hay{{\left( \dfrac{3}{5} \right)}^{2}}+{{\cos }^{2}}\alpha =1 \\
& \Leftrightarrow {{\cos }^{2}}\alpha =1-\dfrac{9}{25}\Leftrightarrow {{\cos }^{2}}\alpha =\dfrac{16}{25}\Rightarrow \cos \alpha =\dfrac{4}{5} \\
& \\
\end{array} $
Câu 18: Cho $ \alpha $ là góc nhọn. Tính $ \sin \alpha ,\cot \alpha $ biết $ \cos \alpha =\dfrac{2}{5} $ .
- A
- B
- C
- D
Ta có $ {{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\Rightarrow {{\sin }^{2}}\alpha =1-{{\cos }^{2}}\alpha =1-\dfrac{4}{25}=\dfrac{21}{25} $ $ \Rightarrow \sin \alpha =\dfrac{\sqrt{21}}{5} $ .
Lại có $ \cot \alpha =\dfrac{\cos \alpha }{\sin \alpha }=\dfrac{\dfrac{2}{5}}{\dfrac{\sqrt{21}}{5}}=\dfrac{2}{\sqrt{21}} $ .
Vậy $ \sin \alpha =\dfrac{\sqrt{21}}{5};\cot \alpha =\dfrac{2}{\sqrt{21}} $ .
Câu 19: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ có $ AC=15cm,CH=6cm $ . Tính tỉ số lượng giác $ \cos B $ .
- A
- B
- C
- D
Xét tam giác $ AHC $ vuông tại $ H $ , theo định lý Pytago ta có $ A{{H}^{2}}=A{{C}^{2}}-C{{H}^{2}}={{15}^{2}}-{{6}^{2}}=189\Rightarrow AH=3\sqrt{21}\Rightarrow \sin C=\dfrac{AH}{AC}=\dfrac{3\sqrt{21}}{15}=\dfrac{\sqrt{21}}{5} $
Mà tam giác $ ABC $ vuông tại $ A $ nên $ \widehat{B},\widehat{C} $ là hai góc phụ nhau. Do đó $ \cos B=\sin C=\dfrac{\sqrt{21}}{5} $ .
Câu 20: Cho tam giác $ ABC $ vuông tại $ A $ . Hãy tính $ \tan C $ biết rằng $ \cot B=2 $ .
- A
- B
- C
- D
Vì tam giác $ ABC $ vuông tại $ A $ nên $ \widehat{B}+\widehat{C}=90{}^\circ \Rightarrow \tan C=\cot B=2 $ .