Mặt phẳng toạ độ, trục tung, trục hoành
Lý thuyết về Mặt phẳng toạ độ, trục tung, trục hoành
1. Mặt phẳng toạ độ
Trên mặt phẳng, nếu hai trục $Ox, Oy$ vuông góc và cắt nhau tại gốc $O$ của mỗi trục số, thì ta gọi hệ trục toạ độ $Oxy$
$Ox$ và $Oy$ gọi là các trục toạ độ
– Trục nằm ngang $Ox$ gọi là trục hoành
– Trục thẳng đứng $Oy$ gọi là trục tung.
Giao điểm $O$ gọi là gốc toạ độ. Mặt phẳng có hệ trục toạ độ $Oxy$ gọi là mặt phẳng toạ độ $Oxy$.
2. Toạ độ của một điểm trong mặt phẳng toạ độ
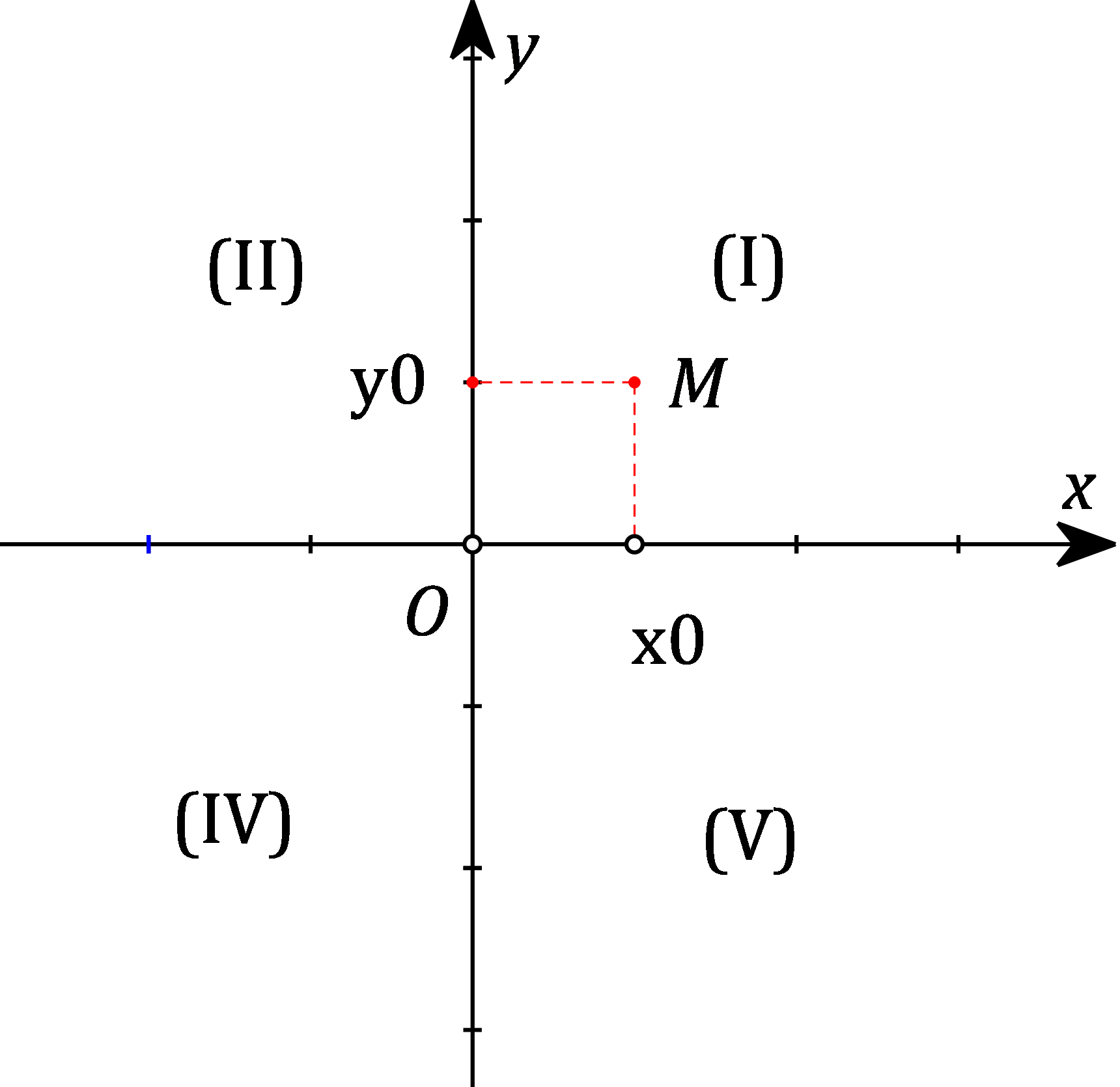
– Trên mặt phẳng toạ độ, mỗi điểm M xác định một cặp số $\left( {{x_0};{y_0}} \right)$. Ngược lại mỗi cặp số $\left( {{x_0};{y_0}} \right)$ xác định vị trí của một điểm $M$.
– Cặp số $\left( {{x_0};{y_0}} \right)$ gọi là toạ độ của điểm $M$; $x_0$ là hoành độ và $y_0$ là tung độ của điểm $M$.
Bài tập tự luyện có đáp án
Câu 1: Cho đồ thị hàm số $ y=f\left( x \right)=4x+\,\,1 $ . Một điểm thuộc đồ thị hàm số có tung độ bằng 5 thì có hoành độ bằng
- A
- B
- C
- D
Với $ y=5\Leftrightarrow 4x+1=5\Leftrightarrow x=1 $ .
Câu 2: Cho các điểm M, N, P có tọa độ như trong hình vẽ. 
Chọn đáp án sai.

Chọn đáp án sai.
- A
- B
- C
- D
Nhìn vào hình vẽ ta thấy: $ M\left( 2;2 \right);\,\, $ $ N\left( -3;0 \right);\,\, $ $ P\left( -2;-3 \right). $
Câu 3: Trên mặt phẳng tọa độ Oxy, các điểm nằm trên trục hoành có tọa độ thỏa mãn:
- A
- B
- C
- D
Trên mặt phẳng tọa độ Oxy thì các điểm nằm trên trục hoành luôn có tung độ bằng 0 và hoành độ là số thực tùy ý.
Câu 4: Chọn đáp án đúng nhất. Trên mặt phẳng tọa độ Oxy, những điểm có hoành độ bằng 2 là:
Trên mặt phẳng tọa độ Oxy, những điểm có hoành độ bằng 2 là:
- A
- B
- C
- D
Trên mặt phẳng tọa độ Oxy, những điểm có hoành độ bằng 2 là những điểm nằm trên đường thẳng song song với trục tung và cắt trục hoành tại điểm có hoành độ bằng 2.
Câu 5: Cho các điểm $ A\left( 2;3 \right) $ và $ B\left( 3;2 \right) $ ; $ M\left( a;b \right) $ và $ N\left( b;a \right) $ . Chọn đáp án sai.
Chọn đáp án sai.
- A
- B
- C
- D
Hai điểm trùng nhau chỉ khi hoành độ của chúng bằng nhau và tung độ của chúng bằng nhau.
Điểm A và điểm B có hoành độ khác nhau và tung độ cũng khác nhau nên không trùng nhau.
Câu 6: Xác định dấu của hoành độ và tung độ điểm $ M\left( x;y \right) $ khi M nằm trong góc phần tư thứ III.
- A
- B
- C
- D
$ M\left( x;y \right) $ nằm trong góc phần tư thứ III khi $ x < 0;y < 0. $
Câu 7: Cho điểm $ A\left( 3;2 \right) $ . Viết tọa độ của điểm B sao cho trục tung là đường trung trực của đoạn thẳng AB.
- A
- B
- C
- D
Để trục tung là đường trung trực của đoạn thẳng AB thì tọa độ điểm B là $ B\left( -3;2 \right). $

Câu 8: Có bao nhiêu điểm phân biệt có tọa độ $ \left( a;b \right) $ thỏa mãn $ a,b\in \left\{ -3;3 \right\}? $
- A
- B
- C
- D
Có điểm có tọa độ $ \left( a,b \right) $ thỏa mãn điều kiện là: $ A\left( -3;-3 \right);\,\,B\left( -3;3 \right);\,\,C\left( 3;-3 \right);\,\,D\left( 3;3 \right). $
Câu 9: Tọa độ của điểm A nằm trên trục tung và có tung độ là 3 là
- A
- B
- C
- D
Điểm A nằm trên trục tung nên có hoành độ bằng 0.
Điểm A có tung độ bằng 3.
Vậy $ A\left( 0;3 \right). $
Xem thêm các bài tiếp theo bên dưới