Tính chất ba đường trung tuyến
Lý thuyết về Tính chất ba đường trung tuyến
Tính chất 3 đường trung tuyến của một tam giác
Định lí: ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng $\dfrac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.
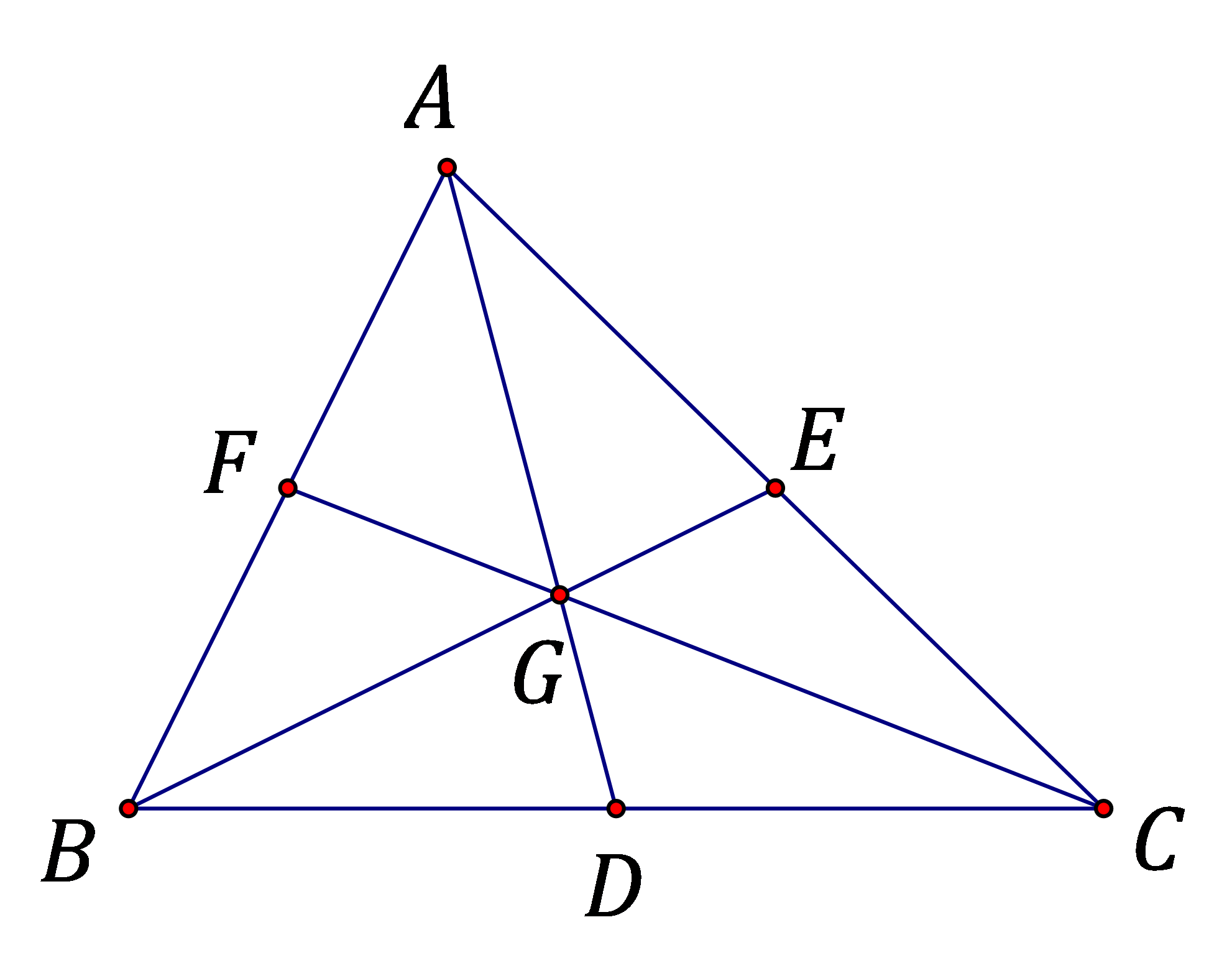
Cụ thể: tam giác $ABC$, các đường trung tuyến $AD,BE,CF$ cùng đi qua điểm $G$ (hay còn gọi là đồng quy tại điểm $G$) và ta có $\dfrac{GA}{DA}=\dfrac{GB}{EB}=\dfrac{GC}{FC}=\dfrac{2}{3}$.
Điểm $G$ gọi là trọng tâm của tam giác $ABC$
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác $ ABC $ đều, trung tuyến $ AM,\text{ }BN,\text{ }CQ $ và $ G $ là trọng tâm. Khẳng định nào dưới đây là sai?
- A
- B
- C
- D
Tam giác $ ABC $ đều nên $ AM=BN=CQ $ và $ AG=\dfrac{2}{3}AM;\,\,\,CG=\dfrac{2}{3}CQ;\,\,\,BG=\dfrac{2}{3}BN $ nên $ GA=GB=GC $ và $ GN=GM=GQ $ ; $ GM=\dfrac{1}{2}AG=\dfrac{1}{2}CG $ .
$ GN=\dfrac{1}{3}BN $ .
Câu 2: Cho tam giác ABC có các đường trung tuyến BM, CN cắt nhau tại G. Cho biết $ BM=CN $ . Khẳng định nào sau đây là sai ?
- A
- B
- C
- D

Vì G là trọng tâm của tam giác ABC nên $ BG=\dfrac{2}{3}BM\,;\,CG=\dfrac{2}{3}CN $ .
Mà $ BM=CN $ nên $ BG=CG $ và $ NG=MG. $
Khi đó: $ \Delta GBN=\Delta GCM\,(c.g.c) $
$ \Rightarrow \,\,BN=CM $ $ \Rightarrow \,\,AB=AC $ $ \Rightarrow \,\Delta ABC $ cân tại A.
Vì G là trọng tâm của tam giác ABC nên AG là đường trung tuyến, tức là AG đi qua trung điểm của BC.
Mà $ \Delta ABC $ cân tại A nên $ AG\bot BC $ .
Câu 3: Cho $ \Delta ABC $ , trung tuyến $ AM $ và $ G $ là trọng tâm của tam giác. Trên tia $ AG $ lấy điểm $ {G}' $ sao cho $ G $ là trung điểm của $ A{G}' $ . Khẳng định nào sau đây là đúng ?
- A
- B
- C
- D
Do $ G $ là trọng tâm của $ \Delta ABC $ nên $ AG=\dfrac{2}{3}AM\Rightarrow GM=\dfrac{1}{2}AG $
Mà $ G $ là trung điểm của $ A{G}' $ nên $ AG=GG' $
$ GM=\dfrac{1}{2}AG=\dfrac{1}{2}GG'\Rightarrow \,M $ là trung điểm đoạn $ GG' $ .
$ \Rightarrow MG'=\dfrac{1}{2}GG'=\dfrac{1}{2}AG $ .
Câu 4: Cho $ \Delta DEF $ có $ DE=DF=5cm,\text{ }EF=6cm $ . Gọi $ I $ là trung điểm của $ EF $ . Độ dài đoạn $ DI $ bằng
- A
- B
- C
- D
Do $ \Delta DEF $ có $ DE=DF\Rightarrow \Delta DEF $ cân tại $ D $
Mà $ I $ là trung điểm của $ EF $ nên $ IE=IF=\dfrac{1}{2}EF=3 $ cm.
Xét tam giác $ \Delta DEI $ và tam giác $ \Delta DFI $ có
$ DE=DF $ , $ DI $ chung, $ EI=FI $
$ \Rightarrow \Delta DEI=\Delta DFI $ (c-c-c)
Ta có $ \widehat{DIE}=\widehat{DIF} $ ( góc tương ứng)
Mà hai góc kề bù nên $ \widehat{DIE}=\widehat{DIF}={{90}^{o}} $
Xét $ \Delta DEI $ có $ DI\bot \,EF $ : $ D{{I}^{2}}+I{{E}^{2}}=D{{E}^{2}} $ (định lí pytago)
$ \Rightarrow DI=\sqrt{D{{E}^{2}}-I{{E}^{2}}}=\sqrt{{{5}^{2}}-{{3}^{2}}}=4 $ cm.
Câu 5: Cho $ \Delta ABC $ cân tại $ A $ . Gọi $ M $ là trung điểm của $ BC $ , độ dài đoạn $ BC=8cm,\,\,\text{ }AC=5cm $ . Độ dài đoạn $ AM $ là
- A
- B
- C
- D
Ta có $ M $ là trung điểm của $ BC $ nên $ BM=CM=\dfrac{1}{2}BC=\,4cm $
Xét tam giác $ \Delta ABM $ và tam giác $ \Delta ACM $ có
$ AB=AC $ , $ AM $ chung, $ BM=CM $
$ \Rightarrow \Delta ABM=\Delta ACM $ (c-c-c)
Ta có $ \widehat{AMB}=\widehat{AMC} $ ( góc tương ứng)
Mà hai góc kề bù nên $ \widehat{AMB}=\widehat{AMC}={{90}^{o}} $
Áp dụng định lí pytago trong tam giác $ \Delta ACM $
$ \begin{array}{l} A{{C}^{2}}=C{{M}^{2}}+A{{M}^{2}}\, \\ \Rightarrow AM\,=\sqrt{A{{C}^{2}}-C{{M}^{2}}}=\sqrt{{{5}^{2}}-{{4}^{2}}}=3cm. \end{array} $
Câu 6: Cho tam giác DEF cân tại D với đường trung tuyến DI. Biết $ DE=DF=13cm,EF=10cm. $ Độ dài đường trung tuyến DI là:
- A
- B
- C
- D

Ta có: $ \Delta DEI=\Delta DFI\left( c.c.c \right)\Rightarrow \widehat{DIE}=\widehat{\text{DIF}}. $
Mà $ \widehat{DIE}+\widehat{\text{DIF}}={{180}^{0}} $ nên $ \widehat{DIE}=\widehat{\text{DIF}}={{90}^{0}}. $
$ IE=\dfrac{1}{2}EF=\dfrac{10}{2}=5\left( cm \right). $
$ \Delta DIE $ vuông tại I nên theo định lí Py-ta-go ta có: $ D{{I}^{2}}=D{{E}^{2}}-I{{E}^{2}}={{13}^{2}}-{{5}^{2}}=169-25=144={{12}^{2}}. $
Vậy $ DI=12cm. $
Câu 7: Cho tam giác ABC với ba trung tuyến AM, BN, CP và trọng tâm G. So sánh nào sau đây là đúng ?
So sánh nào sau đây là đúng ?
- A
- B
- C
- D

Xét $ \Delta GBC $ có: $ GB+GC > BC $ (bất đẳng thức tam giác).
Mặt khác: $ GB=\dfrac{2}{3}BN,GC=\dfrac{2}{3}CP $ (tính chất trọng tâm $ \Delta ABC $ ).
Từ đó, ta có: $ \dfrac{2}{3}BN+\dfrac{2}{3}CP > BC\Leftrightarrow BN+CP > \dfrac{3}{2}BC. $
Câu 8: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Cho biết $ BD < CE. $ Chọn khẳng định đúng.
Chọn khẳng định đúng.
- A
- B
- C
- D

Vì G là trọng tâm của tam giác $ ABC $ nên $ BG=\dfrac{2}{3}BD\,;\,CG=\dfrac{2}{3}CE $ .
Mà $ BD < CE $ nên $ BG < CG\Rightarrow {{\widehat{C}}_{1}} < {{\widehat{B}}_{1}}. $
Vậy $ \widehat{GBC} > \widehat{GCB}. $
Câu 9: Cho tam giác ABC. Trên cạnh BC lấy điểm M sao cho $ BM=2CM. $ Trên tia AC lấy điểm D sao cho C là trung điểm của AD. Gọi N là trung điểm của DB. Khẳng định nào sau đây là sai ?
- A
- B
- C
- D

Xét $ \Delta ABD $ có trung tuyến BC, M là điểm trên BC và $ MB=\dfrac{2}{3}BC $ (do $ BM=2CM $ )
$ \Rightarrow $ M là trọng tâm của $ \Delta ABD $ .
$ \Rightarrow $ M thuộc trung tuyến AN.
$ \Rightarrow $ Ba điểm A, M, N thẳng hàng.
Câu 10: Cho tam giác DEF với ba trung tuyến DM, EN, FP và trọng tâm G. Cho các khẳng định sau:
Chọn.khẳng định đúng.

Chọn.khẳng định đúng.
- A
- B
- C
- D

Tam giác DEF với ba trung tuyến DM, EN, FP và trọng tâm G, ta có:
$ GD=2GM $ ; $ GN=\dfrac{1}{3}EN\,;\,GP=\dfrac{1}{2}GF $ ; $ DM=\dfrac{3}{2}GD. $
Do đó (1) và (4) đúng.
Câu 11: Cho G là trọng tâm của tam giác DEF với đường trung tuyến DH. Trong các khẳng định sau đây, khẳng định nào đúng?
- A
- B
- C
- D

Trong $ \Delta DEF: $ DH là đường trung tuyến, mà G là trọng tâm nên $ \dfrac{GH}{DH}=\dfrac{1}{3}. $
Câu 12: Tam giác ABC có các đường trung tuyến BD và CE bằng nhau. So sánh nào sau đây là đúng ?
So sánh nào sau đây là đúng ?
- A
- B
- C
- D

Gọi G là giao điểm của BD và CE, ta có $ BG=\dfrac{2}{3}BD,CG=\dfrac{2}{3}CE. $
Do $ BD=CE $ nên $ BG=CG,GD=GE. $
$ \Delta BGE=\Delta CGD\left( c.g.c \right)\Rightarrow BE=CD. $
Ta lại có: $ BE=\dfrac{1}{2}AB,CD=\dfrac{1}{2}AC $ nên $ AB=AC. $
Câu 13: Cho tam giác ABC, đường trung tuyến AM. Gọi I là trung điểm của BM. Trên tia đối của IA lấy điểm E sao cho $ IE=IA. $ Điểm M là trọng tâm của tam giác nào sau đây?
- A
- B
- C
- D

Ta có: $ CM=BM=2IM $ (Vì I là trung điểm của BM).
$ \Rightarrow \,CM=\dfrac{2}{3}CI $ .
Xét $ \Delta ACE, $ ta có CI là đường trung tuyến và $ CM=\dfrac{2}{3}CI $
$ \Rightarrow $ M là trọng tâm của tam giác $ ACE $ .
Câu 14: Chọn khẳng định đúng. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền:
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền:
- A
- B
- C
- D

Xét $ \Delta ABC $ vuông tại A, đường trung tuyến AM.
Trên tia đối của tia MA, lấy điểm D sao cho $ MD=MA. $
Ta có: $ AM=\dfrac{1}{2}AD. $ (1)
Dễ thấy: $ \Delta BMD=\Delta CMA\left( c.g.c \right)\Rightarrow BD=AC,{{\widehat{B}}_{1}}=\widehat{C} $ , do đó $ BD//AC. $
Ta lại có: $ \widehat{BAC}={{90}^{0}} $ nên $ \widehat{ABD}={{90}^{0}}. $
Xét $ \Delta CAB $ và $ \Delta DBA $ có:
Cạnh AB chung, $ \widehat{CAB}=\widehat{DBA}={{90}^{0}},AC=BD $
$ \Rightarrow $ $ \Delta CAB=\Delta DBA $ $ \Rightarrow $ $ BC=AD. $ (2)
Từ (1) và (2) suy ra $ AM=\dfrac{1}{2}BC. $