1. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và
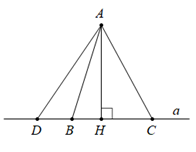
Lý thuyết về 1. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và
1. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
Định lí 1: Trong các đường vuông góc và đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, đường vuông góc ngắn hơn mọi đường xiên.
Ví dụ: AH⊥a⇒AH<AC,AH<ADAH⊥a⇒AH<AC,AH<AD (hình vẽ)
2. Quan hệ giữa đường xiên và hình chiếu
Định lý 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
+ Đường xiên nào có hình chiếu lớn hơn thì lớn hơn
AH⊥a,HD>HC⇒AD>ACAH⊥a,HD>HC⇒AD>AC
+ Đường xiên nào lớn hơn thì có hình chiếu lớn hơn
AH⊥a,AD>AC⇒HD>HCAH⊥a,AD>AC⇒HD>HC
+ Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
AB=AC⇔HB=HCAB=AC⇔HB=HC
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác MNPMNP có ˆM<ˆPˆM<ˆP . Vẽ NK⊥MPNK⊥MP tại KK .
Chọn khẳng định đúng trong các khẳng định sau:
NP > NM(I) NP > NM(I)
KP < KM(II)KP < KM(II)
- A
- B
- C
- D
Xét tam giác MNP có ˆM<ˆP⇒NP<MNˆM<ˆP⇒NP<MN
Ta có NK⊥MPNK⊥MP gt
Mà PK là hình chiếu của PN; KM là hình chiếu của NM nên KP < KMKP < KM .
Câu 2: Cho tam giác DMNDMN vẽ DI⊥MNDI⊥MN tại II , biết rằng IM < INIM < IN . So sánh ˆMˆM và ˆNˆN , ta được kết quả
- A
- B
- C
- D
Xét tam giác DMNDMN
Theo đề bài DI⊥MNDI⊥MN nên I là hình chiếu của điểm D lên MN
⇒IM;IN⇒IM;IN là hình chiếu của DM;DNDM;DN
Mà IM<IN⇒DM<DNIM<IN⇒DM<DN ( quan hệ giữa hình chiếu và đường xiên).
Câu 3: Cho hai đường thẳng d và d’ cắt nhau tại O, A là điểm không nằm trên hai đường thẳng d và d’. Gọi OH và OH’ lần lượt là hình chiếu của OA trên đường thẳng d và đường thẳng d’. Khi đó nếu OH=OH′ thì ta có:
- A
- B
- C
- D

Vì OH và OH’ tương ứng là hình chiếu của OA trên đường thẳng d và đường thẳng d’ nên
AH⊥d tại H, AH′⊥d′ tại H′ .
Xét tam giác AOH và tam giác AOH′ có:
^AHO=^AH′O=90o ; OH=OH′ ; cạnh OA chung
⇒ΔAOH=ΔAOH′ (cạnh huyền, cạnh góc vuông)
⇒AH=AH′ .
Câu 4: Cho tam giác ABC, có AB<AC. Gọi H là hình chiếu của điểm A trên đường thẳng BC. M là điểm bất kì trên đoạn AH. Tia BM cắt cạnh AC tại D. Chọn khẳng định đúng.
Chọn khẳng định đúng.
- A
- B
- C
- D

- So sánh MB và MC .
Ta có: AB<AC nên HB<HC ⇒MB<MC (quan hệ giữa đường xiên và hình chiếu).
- So sánh MD và HD .
Vì ΔMHB vuông tại H ⇒^HMB là góc nhọn.
⇒^DMH là góc tù (hai góc kề bù).
Xét ΔMHD có: ^DMH là góc tù
⇒HD là cạnh lớn nhất (quan hệ góc-cạnh đối diện) hay MD<HD.
Vậy khẳng định đúng là: MD<HD.
Câu 5: Chọn câu trả lời đúng . Cho ΔABC có đường cao AH (HB<HC) , trung tuyến AM . Trên tia đối của tia MA lấy điểm D sao cho MD=MA .
Xét các khẳng định sau:
(I) ΔABM=ΔDCM .
(II) AC>DC .
Cho ΔABC có đường cao AH (HB<HC) , trung tuyến AM . Trên tia đối của tia MA lấy điểm D sao cho MD=MA .
Xét các khẳng định sau:
(I) ΔABM=ΔDCM .
(II) AC>DC .
- A
- B
- C
- D

Xét tam giác ΔABM=ΔDCM có
AM=MDBM=MC^AMB=^CMD(dd)}⇒ΔABM=ΔDCM(c−g−c)
⇒AB=DC ( 2 cạnh tương ứng )
Tam giác ΔABC có AH là đường cao nên H là hình chiều của A lên BC
⇒HB;HC là hình chiếu của AB;AC .
Mà HB<HC nên AB<AC ( quan hệ giữa hình chiếu và đường xiên ).
Lại có AB=DC nên AC>DC
Vậy cả (I) và (II) đúng.
Câu 6: Cho M là điểm nằm trong tam giác ABC. Biết rằng AM=AC. So sánh nào sau đây là đúng ?
So sánh nào sau đây là đúng ?
- A
- B
- C
- D

Xét tam giác AMC có AM+AC>MC (theo bất đẳng thức tam giác)
⇒2AM>MC (Vì AM=AC ).
Gọi N là giao điểm của CM và AB ⇒N nằm giữa A và B ⇒AN<AB (1)
Gọi H là hình chiếu của A trên MC.
Vì AM=AC nên HM=HC, mà HM<HN nên HC<HN⇒AC<AN. (2)
Từ (1) và (2) ⇒AC<AB.
Câu 7: Cho hình vẽ, trong đó DC>DB. 
Chọn khẳng định đúng.

Chọn khẳng định đúng.
- A
- B
- C
- D
Đường xiên DC>DB nên hình chiếu HC>HB.
Hình chiếu HC>HB nên đường xiên AC>AB.
Câu 8: Cho tam giác ABC cân tại A, kẻ AH⊥BC(H∈BC). Trên các đoạn thẳng HB và HC, lấy các điểm D và E sao cho BD=CE. Chọn khẳng định đúng.
Chọn khẳng định đúng.
- A
- B
- C
- D

Đường xiên AB=AC nên hình chiếu HB=HC.
Ta lại có: DB=CE⇒HD=HE.
Hình chiếu HD=HE nên đường xiên AD=AE.
Câu 9: Tam giác ABC có ˆC>ˆB. Kẻ AH⊥BC(H∈BC). So sánh nào sau đây là đúng ?
So sánh nào sau đây là đúng ?
- A
- B
- C
- D

ΔAHC có AC là cạnh huyền nên AC>AH.
ΔABC có ˆC>ˆB⇒AB>AC.
Đường xiên AB>AC nên hình chiếu HB>HC.
Câu 10: Cho tam giác ABC có đường cao AH (H∈BC) . Cho biết AB<AC , khi đó:
- A
- B
- C
- D

Xét tam giác AHC có AC là cạnh huyền nên AH<AC.
Ta có: AB<AC⇒HB<HC (quan hệ giữa đường xiên và hình chiếu).
Câu 11: Chọn câu trả lời đúng. Cho tam giác ABC có AB=8cm, AC=6cm, BC=10cm . D, E, F là các điểm trên đường thẳng AB sao cho AD=4cm, AE=2cm, AF=5cm . So sánh các đoạn thẳng CD, CE, CF ta được kết quả
Cho tam giác ABC có AB=8cm, AC=6cm, BC=10cm . D, E, F là các điểm trên đường thẳng AB sao cho AD=4cm, AE=2cm, AF=5cm . So sánh các đoạn thẳng CD, CE, CF ta được kết quả
- A
- B
- C
- D
Xét tam giác ΔABC có
AC2+AB2=BC2 ( do 62+82=102 )
⇒ΔABC vuông tại A
Nên A là hình chiếu của C lên AB
⇒AE;AD;AF là hình chiếu của nên CE;CD;CF .
Mà AD=4cm, AE=2cm, AF=5cm nên AE<AD<AF
Vậy CE<CD<CF ( quan hệ giữa hình chiếu và đường xiên ).
Câu 12: Cho tam giác DEF có ˆD=80o,ˆE=50o , DM⊥EF . So sánh ME và MF , ta được kết quả
- A
- B
- C
- D
Xét tam giác DEF
Ta có ˆF=1800−ˆD−ˆE=1800−800−500=500
Vì ˆD>ˆE=ˆF⇒EF>DF=DE
Theo đề bài DM⊥EF nên M là hình chiếu của điểm D lên EF
⇒ME;MF là hình chiếu của DE;DF
Mà DE=DF nên DE=DF ( quan hệ giữa hình chiếu và đường xiên) .
Câu 13: Cho tam giác ABC có ˆA=70o,ˆB=50o , AH⊥BC . So sánh BH và HC , ta được kết quả
- A
- B
- C
- D
Xét tam giác ABC
Ta có ˆC=1800−ˆA−ˆB=1800−700−500=600
Vì ˆA>ˆC>ˆB⇒BC>AB>AC
Theo đề bài AH⊥BC nên H là hình chiếu của điểm A lên BC
⇒BH;HC là hình chiếu của BA;AC
Mà AB>AC nên BH>HC ( quan hệ giữa hình chiếu và đường xiên) .
Câu 14: Chọn câu trả lời đúng.
Cho hình vẽ bên có AB < AC , AD⊥BC
Xét các khẳng định sau:
(I) ^ABC>^ACB
(II) DB < DC


- A
- B
- C
- D
Xét tam giác ABC có AD⊥BC
Mà AB < AC⇒^ACB<^ABC và DB < DC .
Câu 15: Cho đoạn thẳng AB và I là trung điểm của AB. Qua I kẻ đường thẳng d. Gọi IH và IK lần lượt là hình chiếu của IA và IB trên đường thẳng d.
Chọn khẳng định đúng.
- A
- B
- C
- D

Xét ΔAIH và ΔBIK có:
^AHI=^BKI=90o ;
IA=IB (Vì I là trung điểm của AB);
^AIH=^BIK (đối đỉnh)
⇒ ΔAHI=ΔBKI (cạnh huyền-góc nhọn).
⇒IH=IK (hai cạnh tương ứng).
Câu 16: Cho tam giác ABC vuông tại A có AB= 8cm . Trên đường thẳng AB lấy các điểm D, E sao cho AD= 3cm, AE= 5cm . So sánh các đoạn thẳng CB, CD,CE .
- A
- B
- C
- D
Xét tam giác ABC vuông tại A có
AD<AE<AB (3<5<8) ( giả thiết)
Mà AD;AE;AB lần lượt là hình chiếu của CD;CE;CB
Nên CB>CE>CD ( quan hệ giữa hình chiếu và đường xiên).
Câu 17: Cho các khẳng định sau: (1) Từ một điểm ở ngoài một đường thẳng ta chỉ kẻ được duy nhất một đường vuông góc với đường thẳng đó.
(2) Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc ngắn hơn mọi đường xiên.
(3) Nếu hai điểm có cùng một hình chiếu trên một đường thẳng thì hai điểm ấy trùng nhau.
Khẳng định nào đúng ? Khẳng định nào sai?
(1) Từ một điểm ở ngoài một đường thẳng ta chỉ kẻ được duy nhất một đường vuông góc với đường thẳng đó.
(2) Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc ngắn hơn mọi đường xiên.
(3) Nếu hai điểm có cùng một hình chiếu trên một đường thẳng thì hai điểm ấy trùng nhau.
Khẳng định nào đúng ? Khẳng định nào sai?
- A
- B
- C
- D
- Khẳng định 1 là đúng:
Từ một điểm ở ngoài một đường thẳng ta chỉ kẻ được duy nhất một đường vuông góc với đường thẳng đó.
- Khẳng định 2 là đúng (theo định lí 2 về quan hệ giữa đường xiên và hình chiếu).
- Khẳng định 3 là sai. Chẳng hạn hình vẽ sau:
Hình chiếu của điểm A trên d là H, hình chiếu của B trên d là H nhưng A và B không trùng nhau.

Câu 18: Cho tam giác ABC cân tại A, điểm D thuộc tia đối của tia CB. Khẳng định nào sau đây là đúng ?
Khẳng định nào sau đây là đúng ?
- A
- B
- C
- D

Kẻ AH⊥BC.
Đường xiên AB=AC suy ra hình chiếu HB=HC.
Ta lại có: HD>HC⇒HD>HB.
Hình chiếu HD>HB nên đường xiên AD>AB.
Câu 19: Cho tam giác ABC vuông tại A . Trên đường thẳng AC lấy các điểm D, E, F sao cho AD=13cm, AE=10cm, AF=18cm . So sánh các đoạn thẳng BD, BE, BF .
- A
- B
- C
- D
Xét tam giác ABC vuông ở A nên AB⊥AC
Nên A là hình chiếu của B lên AC
⇒AE;AD;AF là hình chiếu của nên BE;BD;BF .
Mà AD=13cm, AE=10cm, AF=18cm nên AE<AD<AF
Vậy BF>BD>BE ( quan hệ giữa hình chiếu và đường xiên ).