Thể tích của khối lăng trụ
Lý thuyết về Thể tích của khối lăng trụ
Thể tích của khối lăng trụ bằng diện tích mặt đáy nhân với chiều cao của khối lăng trụ đó $$V=S_{\text{đáy}} \cdot h$$
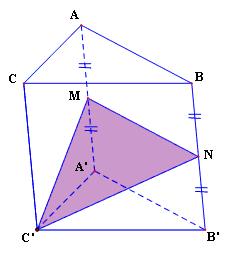
Ví dụ. Cho khối lăng trụ $ABC.A’B’C’$. Gọi $M, N$ lần lượt là trung điểm 2 cạnh $AA’$ và $BB’$. Mặt phẳng $(MNC’)$ 4 chia khối lăng trụ đã cho thành 2 phần. Tính tỉ số thể tích của 2 phần đó
Giải:
Nếu gọi $V$ là thể tích khối lăng trụ thì thể tích khối tứ diện $C’ABC$ là $\dfrac{V}{3}$. Do đó thể tích của khối chóp $C’.ABB’A$ là $\dfrac{2V}{3}$.
Vì 2 khối chóp $C’.ABNM$ và $C’.MNB’A’$ có cùng chiều cao và mặt đáy bằng nhau nên thể tích khối chóp $C’.MNB’A’$ là: $V_1 = \dfrac{1}{2} \cdot \dfrac{2V}{3} = \dfrac{V}{3}$.
Và thể tích khối tứ diện $ABCMNC’$ là: ${{V}_{2}}=V-\dfrac{V}{3}=\dfrac{2V}{3}$.
Ta có tỉ số thể tích hai phần được phân chia là: $k=\dfrac{V_1}{V_2}=\dfrac{1}{2}$.
Bài tập tự luyện có đáp án
Câu 1: Cho hình lăng trụ $ABCD.A'B'C'D'$ có diện tích đáy bằng ${{a}^{2}}$ và khoảng cách từ $d\left( A';\left( ABC \right) \right)=a\sqrt{2}$ . Thể tích khối lăng trụ $ABCD.A'B'C'D'$ bằng
- A
- B
- C
- D
Thể tích khối lăng trụ $ABC{D}.A'B'C'D'$ bằng ${{a}^{2}}.a\sqrt{2}={{a}^{3}}\sqrt{2}$.
Câu 2: Cho lăng trụ tam giác $ABC.A'B'C'$, đáy là tam giác vuông cân tại $A$ có cạnh $AB=a$. Hình chiếu của $A'$ trên mặt phẳng $\left( ABC \right)$ là trung điểm $M$ của cạnh $AB$, $\Delta A'MA$ vuông cân tại $M$. Thể tích khối chóp $ABC.A'B'C'$ là
- A
- B
- C
- D

Ta có $\Delta A'MA$ vuông cân tại $M\Rightarrow A'M=AM=\dfrac{a}{2}$.
${{V}_{ABC.A'B'C'}}=A'M.{{S}_{ABC}}=\dfrac{1}{2}A'M.AB.AC=\dfrac{{{a}^{3}}}{4}$.
Câu 3: Cho hình lăng trụ tứ giác đều $ABC {D}.A'B'C'D'$ có độ dài cạnh đáy là $a$ và $\Delta A'AC$ vuông cân tại $A$ . Thể tích lăng trụ $ABC {D}.A'B'C'D'$ bằng
- A
- B
- C
- D

$\Delta A'AC$ vuông cân tại $A\Rightarrow AA'=AC=a\sqrt{2}$
$\Rightarrow {{V}_{ABCD.A'B'C'D'}}={{a}^{3}}\sqrt{2}$
Câu 4: Cho hình lập phương $ABCD.A'B'C'D'$ . Khẳng định nào sau đây luôn đúng?
- A
- B
- C
- D
Xem thêm các bài tiếp theo bên dưới