Số cực đại, cực tiểu giữa 2 nguồn ngược pha
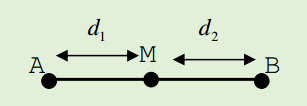
Lý thuyết về Số cực đại, cực tiểu giữa 2 nguồn ngược pha
Phương trình giao thoa sóng tại M: ${{u}_{M}}={{u}_{1M}}+{{u}_{2M}}$
${{u}_{M}}=2Ac\text{os}\left[ \pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\dfrac{\Delta \varphi }{2} \right]c\text{os}\left[ 2\pi ft-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda }+\dfrac{{{\varphi }_{1}}+{{\varphi }_{2}}}{2} \right]$
Biên độ dao động tại M: ${{A}_{M}}=2A\left| c\text{os}\left( \pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\dfrac{\Delta \varphi }{2} \right) \right|$ với $\Delta \varphi =\left| {{\varphi }_{1}}-{{\varphi }_{2}} \right|$
Biên độ phụ thuộc vào hiệu đường truyền và độ lệch pha.
2 nguồn ngược pha pha: ${{u}_{M}}=2Ac\text{os}\left[ \pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\dfrac{\pi }{2} \right]c\text{os}\left[ 2\pi ft-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda }+\dfrac{\pi }{2} \right]$
Trung trực là cực tiểu giao thoa.
$AB=\ell$
M dao động với biên độ cực đại: ${{A}_{\max }}=2A\Leftrightarrow \cos \left( \dfrac{\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right)+\dfrac{\pi }{2} \right)=\pm 1\Leftrightarrow \dfrac{\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right)+\dfrac{\pi }{2}=k\pi \Rightarrow {{d}_{2}}-{{d}_{1}}=\left( 2k+1 \right)\dfrac{\lambda }{2}$
Mà ${{d}_{1}}+{{d}_{2}}=\ell $$\Rightarrow {{d}_{2}}=\dfrac{\ell }{2}+\left( 2k+1 \right)\dfrac{\lambda }{4}$
Mặt khác: $M\in \ell \Rightarrow 0<{{d}_{2}}<\ell \Rightarrow \dfrac{-\ell }{\lambda }-\dfrac{1}{2}<k<\dfrac{\ell }{\lambda }-\dfrac{1}{2}$
M dao động với biên độ cực tiểu (không dao động): ${{A}_{\min }}=0\Leftrightarrow \cos \left( \dfrac{\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right)+\dfrac{\pi }{2} \right)=0\Leftrightarrow \dfrac{\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right)+\dfrac{\pi }{2}=\dfrac{\pi }{2}+k\pi \Rightarrow {{d}_{2}}-{{d}_{1}}=k\lambda $
Mà ${{d}_{1}}+{{d}_{2}}=AB$ $\Rightarrow {{d}_{2}}=\dfrac{AB}{2}+\dfrac{k\lambda }{2}$
Mặt khác: $M\in \ell \Rightarrow 0<{{d}_{2}}<\ell \Rightarrow \dfrac{-\ell }{\lambda }<k<\dfrac{\ell }{\lambda }$
2 cực đại hoặc 2 cực tiểu liên tiếp cách nhau $\frac{\lambda }{2}$
1 cực đại và 1 cực tiểu liên tiếp cách nhau $\frac{\lambda }{4}$
Bài tập tự luyện có đáp án
Câu 1: Chọn câu đúng. Trong hiện tượng giao thoa cuẩ 2 nguồn kết hợp cùng pha, những điểm đứng yên không dao động thì:
- A
- B
- C
- D
Những điểm mà tại đó sóng không dao động là
$Δφ = (2n + 1)π$ với n nguyên ⟹ $Δ = (n + 1/2)λ$ với $Δ = d_2 - d_1$ hoặc $d_1 - d_2$ tùy theo quy ước ban đầu.
Xem thêm các bài tiếp theo bên dưới