Kết quả giao thao ánh sáng
Lý thuyết về Kết quả giao thao ánh sáng
Giao thoa ánh sáng là sự tổng hợp của hai hay nhiều sóng ánh sáng kết hợp trong không gian trong đó xuất hiện những vạch sáng và những vạch tối xen kẽ nhau.
Các vạch sáng (vân sáng) và các vạch tối (vân tối) gọi là vân giao thoa.
+ Hiệu đường đi của ánh sáng (hiệu quang trình)
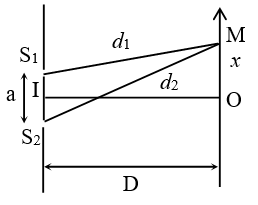
$\Delta d={{d}_{2}}-{{d}_{1}}=\dfrac{\text{ax}}{D}$
Trong đó: $a={{S}_{1}}{{S}_{2}}$ là khoảng cách giữa hai khe sáng
D = OI là khoảng cách từ hai khe sáng ${{S}_{1}},{{S}_{2}}$ đến màn quan sát
${{S}_{1}}M={{d}_{1}};{{S}_{2}}M={{d}_{2}}$
x = OM là (toạ độ) khoảng cách từ vân trung tâm đến điểm M ta xét
+ Vị trí (toạ độ) vân sáng: $\Delta d=k\lambda $ $\Rightarrow$ vị trí vân sáng bậc k: $x=k\dfrac{\lambda D}{a}=ki\text{; }k\in Z$
k = 0: Vân sáng trung tâm
$k=\pm 1:$ Vân sáng bậc (thứ) 1
$k=\pm 2:$ Vân sáng bậc (thứ) 2
+ Vị trí (toạ độ) vân tối: $\Delta d=\left( k+0,5 \right)\lambda $ $\Rightarrow$ Vị trí vân tối thứ k: $x=(k-0,5)\dfrac{\lambda D}{a}=(k-0,5)i;\text{ }k\in Z$
k = 0, k = -1: Vân tối thứ (bậc) nhất
k = 1, k = -2: Vân tối thứ (bậc) hai
k = 2, k = -3: Vân tối thứ (bậc) ba
+ Khoảng vân là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp: $i=\dfrac{\lambda D}{a}$.
+ Khoảng cách giữa 1 vân tối và 1 vân sáng liên tiếp là $\dfrac{i}{2}$
+ Tần số ánh sáng: $f = \dfrac{c}{\lambda }(Hz)$ không đổi khi ánh sáng truyền từ môi trường trong suốt này sang môi trường trong suốt khác.
+ Nếu thí nghiệm được tiến hành trong môi trường trong suốt có chiết suất n thì bước sóng và khoảng vân:
${{\lambda }_{n}}=\dfrac{\lambda }{n}\Rightarrow {{i}_{n}}=\dfrac{{{\lambda }_{n}}D}{a}=\dfrac{i}{n}$
Bài tập tự luyện có đáp án
Câu 1: Trong thí nghiệm giao thoa Young về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng có bước sóng $ \lambda $ . Nếu tại điểm M trên màn quan sát có vân tối thứ 3 ( tính từ vân sáng trung tâm) thì hiệu đường đi của ánh sáng đến hai khe đến M có độ lớn bằng
- A
- B
- C
- D
Ta có M là vân tối: $ {{d}_{1}}-{{d}_{2}}=(k-\dfrac{1}{2})\lambda =(3-\dfrac{1}{2}).\lambda =2,5\lambda $
Câu 2: Trong thí nghiệm giao thoa Iâng, bước sóng ánh sáng đơn sắc dùng cho thí nghiệm là $ 0,59\mu m $ . Tại điểm M trong vùng giao thoa trên màn mà hiệu khoảng cách đến hai khe là $ 1,475\mu m $ có vân
- A
- B
- C
- D
Giả sử tại điểm M trên vùng giao thoa là vân sáng: $ {{d}_{1}}-{{d}_{2}}=k\lambda $ $ \Rightarrow k=\dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda }=\dfrac{1,{{475.10}^{-6}}}{0,{{59.10}^{-6}}}=2,5 $
Vậy tại M là vân tối thứ 3
Câu 3: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc. Nếu tại điểm M trên màn quan sát là vân sáng thì hiệu đường đi của ánh sáng từ hai khe $S_1, S_2$ đến M bằng
- A
- B
- C
- D
Tại M là vân sáng khi hiệu đường truyền ${{d}_{2}}-{{d}_{1}}=k\lambda $ với k nguyên
Câu 4: Trong thí nghiệm I - âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc có bước sóng $λ$. Nếu tại điểm M trên màn quan sát có vân tối thứ hai (tính từ vân sáng trung tâm) thì hiệu đường đi của ánh sáng từ hai khe $S_1, S_2$ đến M có độ lớn bằng
- A
- B
- C
- D
Tại M là vân tối thứ k = 2 vậy: $d_2 – d_1 = (2 – 0,5)\lambda = 1,5\lambda $
Câu 5: Chọn phương án đúng khi nói về chiết suất của một môi trường.
- A
- B
- C
- D
Chiết suất của lăng kính phụ thuộc vào bước sóng của ánh sáng đơn sắc dưới dạng:
$n(\lambda) = A + \dfrac{B}{\lambda^2}+ \dfrac{C}{\lambda^4}+ ...$
Với A, B, C là các hệ số.
Câu 6: Vị trí vân sáng trong thí nghiệm giao thoa của Young được xác định bằng công thức nào sau đây?
- A
- B
- C
- D
Vị trí vân sáng trong thí nghiệm giao thoa của I-âng được xác định bằng công thức
\(x=\dfrac{{k\lambda D}}{a}.\)
Câu 7: Tìm phát biểu đúng về vân giao thoa. Tại vị trí có vân tối thì
- A
- B
- C
- D
Hiệu quang trình đến hai nguồn kết hợp thoả mãn:
$d_2 - d_1 = (2k + 1)\dfrac{\lambda }{2}$,với k nguyên.
Câu 8: Điều nào sau đây là đúng với khái niệm khoảng vân?
- A
- B
- C
- D
Khoảng vân là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp hoặc khoảng cách nhỏ nhất giữa hai vân sáng.
Câu 9: Chọn câu đúng. Một chùm sáng đơn sắc truyền từ không khí vào nước thì
- A
- B
- C
- D
Ánh sáng đặc trưng bởi tần số. Nên khi truyền vào trong các môi trường trong suốt khác nhau thì đại lượng tần số là không đổi. Mặt khác chiết suất tỉ lệ nghịch với bước sóng nên khi ánh sáng truyền vào môi trường chiết quang hơn thì bước sóng của ánh sáng sẽ giảm đi.
Câu 10: Chọn phát biểu đúng. Giao thoa ánh sáng qua kính lọc sắc là hiện tượng …
- A
- B
- C
- D
Giao thoa ánh sáng qua kính lọc sắc là giao thoa của 2 sóng ánh sáng đơn sắc kết hợp. Khi đó xuất hiện các vạch sáng tối xen kẽ trong vùng gặp nhau của 2 sóng.
Câu 11: Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc, khoảng vân đo được trên màn quan sát là 1,14mm. Trên màn, tại điểm M cách vân trung tâm một khoảng 6,27mm có
- A
- B
- C
- D
Ta có: $ \dfrac{x}{i}=\dfrac{6,27}{1,14}=5,5=k+0,5 $ → vân tối thứ k +1 = 6
Câu 12: Thực hiện thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc màu vàng ta quan sát được hệ vân giao thoa trên màn. Nếu thay ánh sáng đơn sắc màu vàng bằng ánh sáng đơn sắc màu lam và các điều kiện khác của thí nghiệm được giữ nguyên thì
- A
- B
- C
- D
Ta có $i=\dfrac{\lambda D}{a}$ mà ${{\lambda }_{v}}>{{\lambda }_{l}}\Rightarrow {{i}_{v}}>{{i}_{l}}$ Vậy khoảng vân giảm xuống.
Câu 13: Nếu làm thí nghiệm Young với ánh sáng trắng thì:
- A
- B
- C
- D
Do các vân bậc càng cao có độ rộng càng lớn vì vậy chúng sẽ đan xen vào nhau và rất khó nhận diện. Nên ta chỉ có thể quan sát được những vân bậc thấp và vân trung tâm.
Câu 14: Gọi $ {{\lambda }_{ch}},{{\lambda }_{c}},{{\lambda }_{l}},{{\lambda }_{v}} $ lần lượt là bước sóng của các tia chàm, cam, lục, vàng. Sắp xếp thứ tự nào dưới đây là đúng?
- A
- B
- C
- D
Thứ tự đúng là $ {{\lambda }_{c}} > {{\lambda }_{v}} > {{\lambda }_{l}} > {{\lambda }_{ch}} $
Câu 15: Cho các loại ánh sáng sau:
I. Ánh sáng trắng.
II. Ánh sáng đỏ.
III. Ánh sáng vàng.
IV. Ánh sáng tím.
Khi thực hiện giao thoa ánh sáng với các loại ánh sáng II, III và IV, hình ảnh giao thoa của loại nào có khoảng vân nhỏ nhất và lớn nhất? Chọn câu trả lời đúng theo thứ tự.
I. Ánh sáng trắng.
II. Ánh sáng đỏ.
III. Ánh sáng vàng.
IV. Ánh sáng tím.
Khi thực hiện giao thoa ánh sáng với các loại ánh sáng II, III và IV, hình ảnh giao thoa của loại nào có khoảng vân nhỏ nhất và lớn nhất? Chọn câu trả lời đúng theo thứ tự.
- A
- B
- C
- D
Trong ba loại ánh sáng đỏ vàng tím thì ánh sáng đỏ có bước sóng dài nhất còn ánh sáng tím có bước sóng ngắn nhất. Theo công thức tính khoảng vân ta thấy khoảng vân tỉ lệ thuận với bước sóng ánh sáng. Do đó khoảng vân đối với ánh sáng đỏ sẽ lớn nhất còn khoảng vân đối với ánh sáng tím sẽ nhỏ nhất.
Câu 16: Trong thí nghiệm giao thoa Y-âng với ánh sáng đơn sắc co khoảng vân là i. Tìm phát biểu không đúng
- A
- B
- C
- D
Vân tối thứ nhất nằm giữa vân sáng bậc 0 và vân sáng bậc 1
Câu 17: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc. Nếu tại điểm M trên màn quan sát là vân tối thì hiệu đường đi của ánh sáng từ hai khe \[S_1, S_2\] đến M bằng
- A
- B
- C
- D
Tại M là vân tối khi ${{d}_{2}}-{{d}_{1}}=(2k+1)\dfrac{\lambda }{2}=(k+0,5)\lambda $ với k nguyên
Câu 18: Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc. Gọi i là khoảng vân, trên màn quan sát, vân tối gần vân sáng trung tâm nhất cách vân sáng trung tâm một khoảng
- A
- B
- C
- D
Vị trí vân tối: $ {{x}_{t}}=\left( k+0,5 \right)i\Rightarrow {{x}_{t-\min }}=0,5i $
Câu 19: Từ hiện tượng tán sắc và giao thoa ánh sáng, kết luận nào sau đây là đúng khi nói về chiết suất của một môi trường?
- A
- B
- C
- D
* Từ hiện tượng tán sắc ánh sáng ta thấy tia đỏ bị lệch ít hơn tia tím hay $D_{đỏ} < D{tím}$ tức là $n_đ < n_t$ do D = (n - 1)A
* Mặt khác nhờ hiện tượng giao thoa ánh sáng chứng minh được ánh sáng tím có bước sóng nhỏ hơn ánh sáng đỏ.
⇒ Từ hai lập luận này ta kết luận ánh sáng có bước sóng ngắn hơn thì chiết suất của môi trường với ánh sáng đó là lớn hơn.
Câu 20: Trong thí nghiệm Young về giao thoa ánh sáng với ánh sáng đơn sắc, vân tối là …
- A
- B
- C
- D
Xem lại bài giao thoa ánh sáng, chú ý phần sự tạo thành các vân giao thoa. Chú ý khái niệm quang trình trong trường hợp tổng quát không trùng với khái niệm khoảng cách từ điểm xét tới nguồn _ hai khái niệm đó chỉ trùng nhau khi ánh sáng truyền trong môi trường đồng tính, có vận tốc xác định.
Câu 21: Thực hiện giao thoa với ánh sáng trắng, trên màn quan sát thu được hình ảnh như thế nào? Chọn kết quả đúng trong các kết quả sau:
- A
- B
- C
- D
Khi sử dụng nguồn sáng là ánh sáng trắng thì tại vị trí trung tâm sẽ có một vân sáng trắng hai bên là những giải màu biến thiên từ đỏ đến tím
Câu 22: Trong thí nghiệm giao thoa Young, vân sáng bậc nhất xuất hiện ở trên màn tại các vị trí mà hiệu đường đi của ánh sáng từ hai nguồn đến các vị trí đó bằng
- A
- B
- C
- D
Vân sáng bậc nhất xuất hiện ở trên màn tại các vị trí mà hiệu đường đi của ánh sáng từ hai nguồn đến các vị trí đó bằng: $ {{d}_{1}}-{{d}_{2}}=k\lambda =1.\lambda =\lambda $
Câu 23: Câu nào sau đây sai khi nói về hiện tượng giao thoa ánh sáng đơn sắc của Young.
- A
- B
- C
- D
Trong thí nghiệm Young với ánh sáng đơn sắc thì ta chỉ có thể thu được hệ vân gồm những vân sáng có màu đặc trung cho ánh sáng đơn sắc và những vân tối.
Câu 24: Công thức tính khoảng vân giao thoa trong thí nghiệm giao thoa của Yâng là
- A
- B
- C
- D
Khoảng vân giao thoa được tính bằng công thức: $ i=\dfrac{\lambda D}{\text{a}} $
Câu 25: Trong thí nghiệm giao thoa ánh sáng Young. Nguồn phát ra ánh sáng đơn sắc có bước sóng λ. Khoảng vân i đo được trên màn sẽ tăng lên khi.
- A
- B
- C
- D
Ta có khoảng vân
\(i = \dfrac{{\lambda D}}{a}\) D tăng thì i tăng.
Câu 26: Trong thí nghiệm Iâng về giao thoa với ánh sáng đơn sắc. Tại vị trí vân tối, tức là hai sóng ánh sáng giao thoa bị triệt tiêu lẫn nhau. Lúc đó ta nói rằng tại vị trí này:
- A
- B
- C
- D
Điều kiện thỏa mãn là hai sóng đó phải là hai sóng kết hợp và hiệu số pha của hai sóng tại vị trí đang xét phải là một đại lượng không đổi và bằng π.
Câu 27: Trong thí nghiệm giao thoa Young khoảng cách giữa 2 khe là a, khoảng cách giữa mặt phẳng hai khe đến màn là D, giao thoa với ánh sáng đơn sắc có bước sóng \[ \lambda \] . Vị trí vân tối thứ k được xác định theo công thức nào sau đây?
- A
- B
- C
- D
Vị trí vân tối bậc k được xác định theo công thức: $ x=\left( k+0,5 \right)\dfrac{\lambda D}{a} $
Với k nguyên, a là khoảng cách giữa 2 khe, D là khoảng cách giữa mặt phẳng hai khe đến màn, \[ \lambda \] là bước sóng
Câu 28: Công thức tính khoảng vân giao thoa là
- A
- B
- C
- D
Công thức tính khoảng vân giao thoa là
\(i=\dfrac{{\lambda D}}{a}.\)
Câu 29: Nguyên lý giao thoa cần để giải thích thỏa đáng điều nào sau đây:
I. Hiện tượng tán sắc ánh sáng.
II. Sự sản sinh màu xanh của lá.
III. Sự xuất hiện của váng dầu.
IV. Sự xuất hiện của ảnh ảo thay vì ảnh thật trong gương phẳng.
I. Hiện tượng tán sắc ánh sáng.
II. Sự sản sinh màu xanh của lá.
III. Sự xuất hiện của váng dầu.
IV. Sự xuất hiện của ảnh ảo thay vì ảnh thật trong gương phẳng.
- A
- B
- C
- D
Nguyên lí của hiện tượng giao thoa có thể dùng để giải thích hiện tượng tán sắc ánh sáng và sự xuất hiện của váng dầu.
Câu 30: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc có bước sóng $ \lambda $. Nếu tại điểm M trên màn quan sát có vân tối thì hiệu đường đi của ánh sáng từ hai khe đến điểm M có độ lớn nhỏ nhất bằng
- A
- B
- C
- D
Tại M là vân tối nên: $∆d = d_2 – d_1 = (k – 0,5) \lambda $ (với k nguyên).
$∆d_{min} = 0,5 \lambda $ khi k = 1
Câu 31: Trong thí nghiệm giao thoa Y-âng khoảng cách giữa 2 khe là a, khoảng cách giữa mặt phẳng hai khe đến màn là D, giao thoa với ánh sáng đơn sắc có bước sóng $ \lambda $ , vị trí vân sáng bậc k được xác định theo công thức nào sau đây
- A
- B
- C
- D
Vị trí vân sáng bậc k được xác định theo công thức: $ x=k\dfrac{\lambda D}{a} $
Với k nguyên, a là khoảng cách giữa 2 khe, D là khoảng cách giữa mặt phẳng hai khe đến màn, $ \lambda $ là bước sóng
Xem thêm các bài tiếp theo bên dưới