Mạch R,L,C nối tiếp
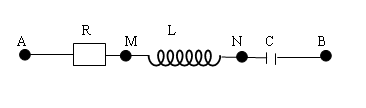
Lý thuyết về Mạch R,L,C nối tiếp
Cường độ dòng điện trong mạch: i=I0cosωt
Điện áp tức thời 2 đầu mỗi phần tử:
uR=U0Rcosωt(U0R=Io.R)
uL=U0Lcos(ωt+π2)(U0L=I0.ZL)
uC=U0Ccos(ωt−π2)(U0C=I0.ZC)
Điện áp tức thời 2 đầu đoạn mạch: uAB=uR+uL+uC⇔→uAB=→uR+→uL+→uC
Giản đồ vec tơ:
uAB=U0cos(ωt+φ)
Z=√R2+(ZL−ZC)2⇒U=√U2R+(UL−UC)2⇒U0=√U20R+(U0L−U0C)2
tanφ=ZL−ZCR;sinφ=ZL−ZCZ;cosφ=RZ với −π2≤φ≤π2
I=UZ;I0=U0Z ;
ZL=ωL(Ω) ;
ZC=1ωC
Trong đó:
+ UR=I.R;UC=I.ZC;UL=I.ZL là HĐT hiệu dụng 2 đầu điện trở, tụ điện và cuộn cảm.
+ U0R=I0.R;U0C=I0.ZC;U0L=I0.ZL là HĐT cực đại 2 đầu điện trở và tụ điện và cuộn cảm.
+ ZC;ZL;R là dung kháng ; cảm kháng và điện trở.
* Khi ZL>ZC hay ω>1√LC ⇒φ>0 thì u nhanh pha hơn i
* Khi ZL<ZC hay ω<1√LC ⇒φ<0 thì u chậm pha hơn i
* Khi ZL=ZC hay ω=1√LC ⇒φ=0 thì u cùng pha với i.
Bài tập tự luyện có đáp án
Câu 1: Đặt một điện áp xoay chiều có giá trị hiệu dụng không đổi vào hai đầu đoạn mạch gồm điện trở R, cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C. Điện áp giữa hai đầu
- A
- B
- C
- D
Điện áp giữa hai đầu cuộn dây luôn ngược pha với điện áp giữa hai đầu tụ điện.
Câu 2: Đoạn mạch điện xoay chiều có R,L,C nối tiếp sẽ xảy ra cộng hưởng điện nếu
- A
- B
- C
- D
Cộng hưởng điện xảy ra khi ZC=ZL
khi đó Z = R.
Câu 3: Đặt điện áp xoay chiều u=U√2cos(ωt+φ) (ω > 0) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Gọi Z và I lần luợt là tổng trở của đoạn mạch và cường độ dòng điện hiệu dụng trong đoạn mạch. Hệ thức nào sau đây đúng?
Đặt điện áp xoay chiều u=U√2cos(ωt+φ) (ω > 0) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Gọi Z và I lần luợt là tổng trở của đoạn mạch và cường độ dòng điện hiệu dụng trong đoạn mạch. Hệ thức nào sau đây đúng?
- A
- B
- C
- D
U=IZ
Câu 4: Công thức tính tổng trở của đoạn mạch RLC mắc nối tiếp là
- A
- B
- C
- D
Công thức tính tổng trở của đoạn mạch RLC mắc nối tiếp là
Z=√R2+(ZL−ZC)2.
Câu 5: Đoạn mạch điện xoay chiều gồm điện trở thuần R, cuộn cảm thuần L và tụ điện C mắc nối tiếp. Kí hiệu uR,uL,uC tương ứng là điện áp tức thời ở hai đầu các phần tử R, L và C. Quan hệ về pha của các điện áp này là
- A
- B
- C
- D
uC và uL ngược pha.
Câu 6: Đặt vào hai đầu đoạn mạch RLC không phân nhánh một hiệu điện thế xoay chiều u=U0cosωt thì dòng điện trong mạch là i=I0cos(ωt+π6)A . Đoạn mạch điện này luôn có
- A
- B
- C
- D
u chậm pha π/6 so với i, do đó mạch RLC này có tính dung kháng
Câu 7: Trong mạch RLC mắc nối tiếp, độ lệch pha giữa dòng điện và hiệu điện thế giữa hai đầu đoạn mạch phụ thuộc vào
- A
- B
- C
- D
Độ lệch pha giữa cường độ dòng điện và hiệu điện thế được tính theo công thức
tanφ=ZL−ZCR
tức là φ phụ thuộc vào R, L, C và f (bản chất của mạch điện).
Câu 8: Một đoạn mạch RLC mắc nối tiếp. Biết rằng U0C=U0L thì hiệu điện thế giữa hai đầu đoạn mạch và dòng điện sẽ:
- A
- B
- C
- D
Theo bài ra thì : U0C=U0L⇒ZL=ZC hay tgφ = 0 tức là i và u cùng pha.
Câu 9: Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cuộn cảm có cảm kháng ZLvà tụ điện có dung khángZC. Tổng trở của đoạn mạch là:
- A
- B
- C
- D
√R2+(ZL−ZC)2
Câu 10: Đặt điện áp u=U0cosωt (U0 không đổi, ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Tổng trở của mạch là
- A
- B
- C
- D
Tổng trở của mạch là:
Z=√R2+(ZL−ZC)2=√R2+(ωL−1ωC)2
Câu 11: Trong mạch điện xoay chiều có R, L, C mắc nối tiếp. ZL,ZC lần lượt là cảm kháng của dung khách thì tổng trở Z xác định theo công thức
- A
- B
- C
- D
Tổng trở của mạch RLC mắc nối tiếp Z=√R2+(ZL−ZC)2
Câu 12: Mạch điện AB gồm điện trở thuần R = 50Ω; cuộn dây có độ tự cảm L = 0,4/ π H và điện trở r = 60Ω; tụ điện có điện dung C thay đổi được mắc nối tiếp theo đúng thứ tự trên vào điện áp u=220√2cos(100πt)(V) (t tính bằng giây). Người ta thấy rằng khi C=Cm thì điện áp hiệu dụng ở hai đầu đoạn mạch chứa cuộn dây và tụ điện đạt cực tiểu Umin. Giá trị của Cm và Umin lần lượt là
- A
- B
- C
- D
R=50Ω;ZL=40Ω;r=60Ω
ULrC=U√r2+(ZL−ZC)2√(R+r)2+(ZL−ZC)2=U√R+2Rrr2+(ZL−ZC)2+1
Để ULrCmin
Xem thêm các bài tiếp theo bên dưới