Mạch điện xoay chiều chỉ chứa cuộn cảm
Lý thuyết về Mạch điện xoay chiều chỉ chứa cuộn cảm
Cuộn thuần cảm là cuộn cảm lí tưởng không có điện trở thuần ( đặc trưng cho cuộn thuần cảm là độ tự cảm L)
Dòng 1 chiều đi qua được cuộn thuần cảm ( lúc này cuộn như dây dẫn không có điện trở R)
Dòng xoay chiều cũng đi qua cuộn thuần cảm nhưng bị cản trở 1 phần. Đại lượng vật lí đặc trưng cho sự cản trở dòng điện của cuộn cảm là cảm kháng:
${{Z}_{L}}=\omega L\left( \Omega \right)$ $\Rightarrow I=\dfrac{U}{{{Z}_{L}}}$; ${{I}_{0}}=\dfrac{{{U}_{0}}}{{{Z}_{L}}}$
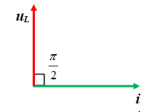
${{u}_{L}}$ nhanh pha hơn i là$\pi /2$ ,$(\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=\pi /2)$
Ta luôn có: \(\dfrac{{{u}^{2}}}{{{U}^{2}}}\ +\ \dfrac{{{i}^{2}}}{{{I}^{2}}}\ =\ 2.\) ; $\dfrac{{{u}^{2}}}{U_{0}^{2}}+\dfrac{{{i}^{2}}}{I_{0}^{2}}=1$
Bài tập tự luyện có đáp án
Câu 1: Đặt điện áp xoay chiều $u=U\sqrt{2}\cos (\omega t+\varphi )$) (U > 0, ω> 0) vào hai đầu cuộn cảm thuần có độ tự cảm L. Cường độ dòng điện hiệu dụng trong cuộn cảm là
Đặt điện áp xoay chiều $u=U\sqrt{2}\cos (\omega t+\varphi )$) (U > 0, ω> 0) vào hai đầu cuộn cảm thuần có độ tự cảm L. Cường độ dòng điện hiệu dụng trong cuộn cảm là
- A
- B
- C
- D
$I=\dfrac{U}{{{Z}_{L}}}=\dfrac{U}{\omega L}.$
Câu 2: Khi dòng điện xoay chiều có tần số 50 Hz chạy trong cuộn cảm thuần có độ tự cảm $\dfrac{1}{2\pi }$H thì cảm kháng của cuộn cảm này bằng
- A
- B
- C
- D
${{Z}_{L}}=\omega L\left( \Omega \right)$ $=2\pi fL=2\pi .50.$ $\dfrac{1}{2\pi }=50 \Omega $
Câu 3: Đặt điện áp xoay chiều $u=U\sqrt{2}\cos (\omega t+\varphi )$ ( ω> 0) vào hai đầu cuộn cảm thuần có độ tự cảm L. Cảm kháng của cuộn cảm này bằng
- A
- B
- C
- D
${{Z}_{L}}=\omega L$
Câu 4: Đặt điện áp xoay chiều có giá trị hiệu dụng 220 V, tần số 50 Hz vào hai đầu một cuộn cảm thuần có độ tự cảm L thì giá trị cực đại của cường độ dòng điện trong đoạn mạch bằng 1 A. Giá trị của L bằng
- A
- B
- C
- D
\(\bullet \text{ f = 50 Hz}\to \omega =100\pi \)
$\bullet \text{ U = 220 V}\to {{U}_{0}}=220\sqrt{2}\text{ }V\to {{Z}_{L}}=\dfrac{{{U}_{0}}}{{{I}_{0}}}=\dfrac{220\sqrt{2}}{1}=220\sqrt{2}\text{ }\Omega \text{ }\to \text{ L = }\dfrac{{{Z}_{L}}}{\omega }=0,99\text{ H}$.
Câu 5: Trong đoạn mạch điện xoay chiều chỉ có cuộn cảm thuần thì hiệu điện thế ở hai đầu đoạn mạch
- A
- B
- C
- D
Trong đoạn mạch điện xoay chiều chỉ có cuộn cảm thuần thì hiệu điện thế ở hai đầu đoạn mạch sớm pha $\dfrac{\pi }{2}$ so với cường độ dòng điện