Thể tích của hình lăng trụ đứng
Lý thuyết về Thể tích của hình lăng trụ đứng
Thể tích hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao.
$V=S.h$ ( $S$ là diện tích đáy, $h$ là chiều cao)
Bài tập tự luyện có đáp án
Câu 1: Một lăng trụ tam giác có đáy là tam giác vuông với hai cạnh góc vuông có độ dài là a, b đồng thời chiều cao của lăng trụ là h. Thể tích lăng trụ là:
- A
- B
- C
- D
Thể tích hình lăng trụ bằng tích của diện tích đáy và chiều cao nên: V= $ \dfrac{1}{2}a.b.h $
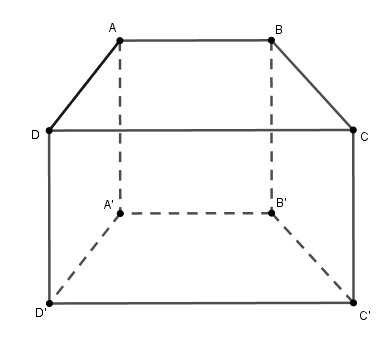
Câu 2:  Cho hình lăng trụ đứng như hình vẽ. Biết rằng mặt đáy là hình thang cân với hai đáy $AB = 10mm$, $CD = 22mm$ và chiều cao $h = 8mm$. Chiều cao của lăng trụ là $h' = 14mm$.
Thể tích của hình lăng trụ là:
Cho hình lăng trụ đứng như hình vẽ. Biết rằng mặt đáy là hình thang cân với hai đáy $AB = 10mm$, $CD = 22mm$ và chiều cao $h = 8mm$. Chiều cao của lăng trụ là $h' = 14mm$.
Thể tích của hình lăng trụ là:
 Cho hình lăng trụ đứng như hình vẽ. Biết rằng mặt đáy là hình thang cân với hai đáy $AB = 10mm$, $CD = 22mm$ và chiều cao $h = 8mm$. Chiều cao của lăng trụ là $h' = 14mm$.
Thể tích của hình lăng trụ là:
Cho hình lăng trụ đứng như hình vẽ. Biết rằng mặt đáy là hình thang cân với hai đáy $AB = 10mm$, $CD = 22mm$ và chiều cao $h = 8mm$. Chiều cao của lăng trụ là $h' = 14mm$.
Thể tích của hình lăng trụ là:- A
- B
- C
- D
Diện tích đáy là $S_{ABCD} = \dfrac{AB + CD}{2} \cdot h = 128 mm^2$
Câu 3: Cho hình lăng trụ đứng có thể tích là V, diện tích đáy là S, vậy chiều cao h được xác định bởi công thức nào sau đây.
- A
- B
- C
- D
Câu 4: Cho hình lăng trụ tam giác đều có cạnh đáy bằng $a$, diện tích một mặt bên là $2a^2$. Thể tích của khối lăng trụ đó là:
- A
- B
- C
- D
Diện tích mặt bên bằng $2a^2$ nên chiều cao của lăng trụ là $h = 2a$.
Diện tích mặt đáy là $S = \dfrac{a^2\sqrt{3}}{4}$.
Câu 5: Một hình lăng trụ đứng có đáy là hình vuông cạnh a. Biết thể tích của hình lăng trụ này là $ {{\text{a}}^{3}}\sqrt{3} $ . Khẳng định nào đúng khi nói về chiều cao của hình lăng trụ.
- A
- B
- C
- D
Gọi chiều cao của lăng trụ đứng là h. Ta có:
$ \text{h = }\dfrac{\text{V}}{S}\text{ = }\dfrac{\text{V}}{{{\text{a}}^{\text{2}}}}\text{ = }\dfrac{{{\text{a}}^{\text{3}}}\sqrt{\text{3}}}{{{\text{a}}^{\text{2}}}}\text{ = a}\sqrt{3}. $
Vậy chiều cao lớn hơn cạnh hình vuông ở mặt đáy, vậy hình lăng trụ không phải hình lập phương.
Câu 6: Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $A$, $AB = a$, $AC = a\sqrt{3}$, $AA' = 2a$. Thể tích của khối lăng trụ $ABC.A'B'C'$ là:
- A
- B
- C
- D
Câu 7:  Thể tích của hình lăng trụ đứng theo các kích thước trong hình là:
Thể tích của hình lăng trụ đứng theo các kích thước trong hình là:
 Thể tích của hình lăng trụ đứng theo các kích thước trong hình là:
Thể tích của hình lăng trụ đứng theo các kích thước trong hình là:- A
- B
- C
- D
Nhận thấy đáy là một tam giác vuông có độ dài hai cạnh góc vuông là $4cm$ và $6cm$ nên diện tích đáy là $S = 12cm^2$.
Khi đó thể tích là $V = Sh = 120 cm^3$.
Câu 8: Cho hình lăng trụ đứng có đáy là tam giác đều cạnh $a$, khoảng cách giữa hai đáy bằng $3a$. Thể tích khối lăng trụ là:
- A
- B
- C
- D