Diện tích xung quanh, diện tích toàn phần của hình lăng trụ đứng
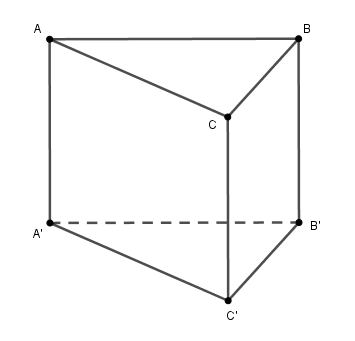
Lý thuyết về Diện tích xung quanh, diện tích toàn phần của hình lăng trụ đứng
Định nghĩa:
- Diện tích xung quanh của hình lăng trụ đứng bằng tổng diện tích của các mặt bên.
- Diện tích toàn phần của lăng trụ đứng bằng tổng diện tích xung quanh và diện tích hai đáy.
Công thức:
- Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với chiều cao.
$S_{xq} = 2ph$, trong đó $p$ là nửa chu vi, $h$ là chiều cao$.
- $$S_{tp} = S_{xq} + 2 \cdot S_{\text{đáy}}.$$
Bài tập tự luyện có đáp án
Câu 1: Hình lăng trụ đứng tam giác có bao nhiêu mặt là hình chữ nhật?
- A
- B
- C
- D
Hình lăng trụ đứng tam giác $ABC.A'B'C'$ có các mặt bên $ABB'A', BCC'B', CAA'B'$ đều là các hình chữ nhật (xem hình vẽ).

Câu 2: Một hình hộp đứng có tối đa bao nhiêu mặt là hình chữ nhật?
- A
- B
- C
- D
Hình hộp đứng $ABCD.A'B'C'D'$ luôn có các mặt bên $ABB'A', BCC'B', CDD'C', DAA'D'$ là các hình chữ nhật. Khi đó nó tối đa có thêm hai mặt đáy $ABCD$, $A'B'C'D$ là các hình chữ nhật. Vậy có tối đa $6$ mặt là hình chữ nhật (xem hình vẽ).

Câu 3: Một hình lăng trụ đứng có ít nhất bao nhiêu đỉnh?
- A
- B
- C
- D
Hình lăng trụ có ít đỉnh nhất chính là lăng trụ tam giác $ABC.A'B'C'$ có 6 đỉnh (xem hình vẽ).

Câu 4: Một lăng trụ đứng, đáy là tam giác thì lăng trụ đó có:
- A
- B
- C
- D
Tham khảo hình vẽ:

Câu 5: Hình hộp đứng $ABCD.A'B'C'D$ có bao nhiêu cặp mặt phẳng song song?
- A
- B
- C
- D
Các cặp mặt phẳng đối diện của hình hộp đứng đều song song với nhau.

Câu 6: Một hình lăng trụ đứng có 10 mặt. Số đỉnh, số cạnh của hình lăng trụ đó là:
- A
- B
- C
- D
Hình lăng trụ đứng có 10 mặt thì có 16 đỉnh và 24 cạnh.
Câu 7: Một cái chặn giấy bằng thủy tinh hinh lăng trụ đứng có các kích thước như hình vẽ.
 Diện tích xung quanh của nó là
Diện tích xung quanh của nó là
 Diện tích xung quanh của nó là
Diện tích xung quanh của nó là- A
- B
- C
- D
Diện tích xung quanh của hình lăng trụ đứng bằng chu vi của đáy nhân với chiều cao.
Câu 8: Diện tích xung quanh của lăng trụ đứng là tổng diện tích của:
- A
- B
- C
- D
Diện tích xung quanh của lăng trụ đứng là tổng diện tích của tất cả các mặt bên của hình lăng trụ đứng.
Câu 9: Một hình lăng trụ đứng có chu vi mặt đáy là 24 cm và chiều cao là 5cm thì có diện tích xung quanh là:
- A
- B
- C
- D
Diện tích xung quanh của hình lăng trụ là: $ 24.5=120\left( c{{m}^{2}} \right) $
Câu 10: Một cái chặn giấy bằng thủy tinh hinh lăng trụ đứng có các kích thước như hình vẽ.
 Diện tích toàn phần của nó là:
Diện tích toàn phần của nó là:
 Diện tích toàn phần của nó là:
Diện tích toàn phần của nó là:- A
- B
- C
- D
Ta có diện tích toàn phần của hình lăng trụ bằng diện tích xung quanh cộng với diện tích của hai mặt đáy.
Câu 11: Diện tích xung quanh của hình lăng trụ đứng được tính bởi
- A
- B
- C
- D
Câu 12: Một hình lăng trụ đứng có đáy là hình thoi với các đường chéo của đáy bằng 16cm và 30cm. Diện tích toàn phần của hình lăng trụ bằng 1840 $ c{{m}^{2}} $ . Diện tích xung quanh hình lăng trụ là.
- A
- B
- C
- D
Diện tích mặt đáy của hình lăng trụ là:
$ 16.30:2=240c{{m}^{2}}. $
Diện tích xung quanh của hình lăng trụ là:
$ 1840-240=1600c{{m}^{2}}. $
Câu 13: Cho hình lăng trụ đứng $ABCD.A'B'C'D'$ có $AB = a, BB' = 2a$. Diện tích toàn phần của hình lăng trụ bằng bao nhiêu?
- A
- B
- C
- D
Chu vi đáy là $4a$, diện tích một mặt đáy bằng $a^2$.
Câu 14:  Diện tích toàn phần của hình lăng trụ đứng theo các kích thước trong hình là
Diện tích toàn phần của hình lăng trụ đứng theo các kích thước trong hình là
 Diện tích toàn phần của hình lăng trụ đứng theo các kích thước trong hình là
Diện tích toàn phần của hình lăng trụ đứng theo các kích thước trong hình là- A
- B
- C
- D
Nhận thấy đáy là một tam giác vuông có độ dài hai cạnh góc vuông là $8cm$ và $6cm$ nên độ dài cạnh huyền còn lại là $10cm$.