Các công thức tính nhanh cực trị hàm bậc ba y=ax3+bx3+cx+d
Lý thuyết về Các công thức tính nhanh cực trị hàm bậc ba y=ax3+bx3+cx+d
Xét hàm số y=ax3+bx2+cx+d(a≠0)
- Hàm số không có cực trị (hay hàm số đơn điệu trên R) khi b2≤3ac.
- Hàm số có hai cực trị khi b2>3ac.
- Đường thẳng đi qua hai điểm cực trị (nếu có) của đồ thị hàm số: y=(2c3−2b29a)x+d−bc9a.
- Giả sử hai điểm cực trị x1,x2. Khi đó: {x1+x2=−2b3ax1x2=c3a|x1−x2|=23|a|√b2−3ac.
- Gọi x1<x2 là hai nghiệm của y′=0.
- Khi a>0 thì x1 là điểm cực đại của hàm số, x2 là điểm cực tiểu của hàm số.
- Khi a<0 thì x1 là điểm cực tiểu của hàm số, x2 là điểm cực đại của hàm số.
Bài tập tự luyện có đáp án
Câu 1: Cho hàm số y=x33−mx22+13 đạt cực tiểu tại x0=2 khi
- A
- B
- C
- D
Ta có: y′=x2−mx⇒y′(2)=4−2m=0⇔m=2
Khi đó y″(2)=2.2−2=2>0 . Do vậy với m=2 thì hàm số đạt cực tiểu tại x=2 .
Câu 2: Hàm số y=13x3+mx2+(m2+2m)x−1 có hai điểm cực trị khi và chỉ khi:
- A
- B
- C
- D
y′=x2+2mx+m2+2m
Hàm số có 2 điểm cực trị khi
Δ′>0⇔m2−(m2+2m)>0⇔m<0
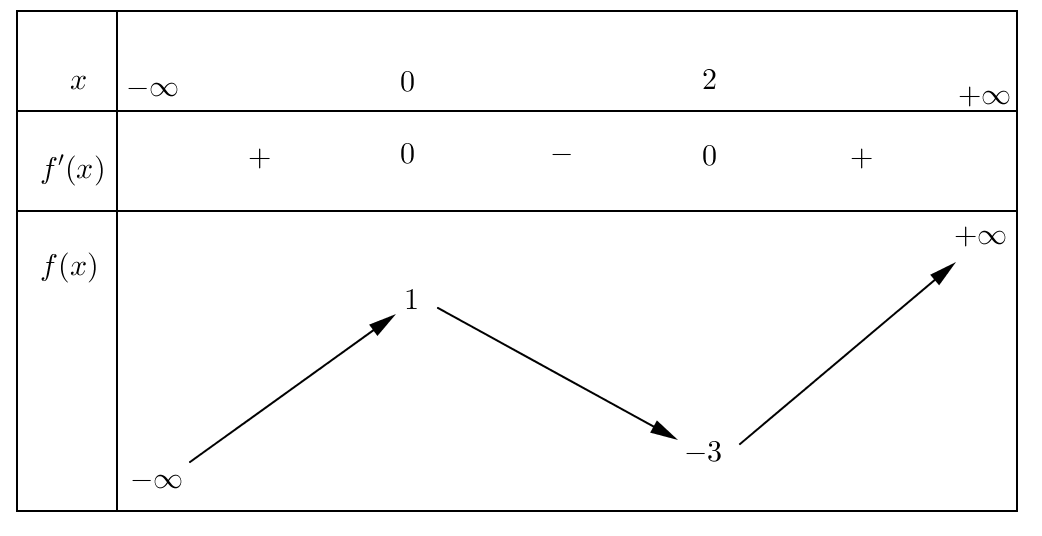
Câu 3: Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình dưới đây:

Mệnh đề nào dưới đây đúng?

Mệnh đề nào dưới đây đúng?
- A
- B
- C
- D
Từ bảng biến thiên suy ra giá trị cực đại của hàm số bằng 1.
Câu 4: Tìm m để hàm số y=x3−3mx2+3(m2−1)x+m đạt cực đại tại x=2
- A
- B
- C
- D
y′=3x2−6mx+3m2−3;y″=6x−6m
YCBT⇔{y′(2)=0y″(2)<0⇔{12−12m+3m2−3=012−6m<0⇔{[m=1m=3m>2⇔m=3 .
Câu 5: Hàm số y=13(m+1)x3+2mx2+(3m+2)x+1 có cực đại, cực tiểu khi và chỉ khi.
- A
- B
- C
- D
y′=(m+1)x2+4mx+3m+2
Hàm số có cực đại cực tiểu khi
{m≠−1Δ′>0⇔{m≠−14m2−(3m+2)(m+1)>0⇔{m≠−1m2−5m−2>0⇔{[m<5−√332m>5+√332m≠−1
Câu 6: Cho hàm số y=−x3+2(m+1)x2+mx+3 . Giá trị của m để hàm số đạt cực tiểu tại điểm x=43 là:
- A
- B
- C
- D
y′=−3x2+4(m+1)x+m;y″=−6x+4m+4
Hàm số đạt cực tiểu tại điểm x=43
⇔{y′(43)=0y″(43)>0⇔{−3.(43)2+4(m+1).43+m=0−6.43+4m+4>0⇔{19m3=04m−4>0⇔{m=0m>1⇔m∈∅
Câu 7: Cho hàm số y=ax3+bx2+cx+d(a≠0). Điều kiện để hàm số có cực trị trên khoảng K là
- A
- B
- C
- D
Hàm bậc ba có cực trị trên khoảng K khi y′=0 có hai nghiệm phân biệt trên K hoặc y′=0 có hai nghiệm phân biệt trong đó có 1 nghiệm thuộc K.
Câu 8: Hàm số y=(m−3)x3−2mx2+3 không có cực trị khi
- A
- B
- C
- D
Ta có m=3⇒y=−6x2+3 hàm số có một điểm cực trị
Với m≠3⇒y′=3(m−3)x2−4mx=0⇔[x=0x=4m3(m−3)
Hàm số không có cực trị ⇔4m3(m−3)=0⇔m=0 .
Câu 9: Giá trị của m để hàm số y=13x3−mx2+(m2−m+1)x+1 đạt cực đại tại điểm x=1 :
- A
- B
- C
- D
y′=x2−2mx+m2−m+1y″=2x−2m
Hàm số đạt cực đại tại x=1
⇔{y′(1)=0y″(1)<0⇔{1−2m+m2−m+1=02−2m<0⇔{[m=1m=2m>1⇔m=2
Câu 10: Cho hàm số y=13x3−mx2+(m2−m−1)x+2 . Tìm m để hàm số đạt cực đại tại x=−1
- A
- B
- C
- D
y′=x2−2mx+m2−m−1;y″=2x−2m
YCBT⇔{y′(−1)=0y″(−1)<0
⇔{1+2m+m2−m−1=0−2−2m<0
⇔{m(m+1)=0m>−1
⇔m=0 .
Xem thêm các bài tiếp theo bên dưới