Điều kiện đủ để hàm số đơn điệu
Lý thuyết về Điều kiện đủ để hàm số đơn điệu
Bài toán 1: Tìm tham số m để hàm số y=ax3+bx2+cx+d đơn điệu trên R.
Phương pháp giải
Bước 1: Tính đạo hàm y′=3ax2+2bx+c .
Bước 2: Xét dấu y′ (khi a≠0).
Hàm số đồng biến trên ⇔y′≥0,∀x∈⇔{ay′>0Δy′≤0m.
Hàm số nghịch biến trên ⇔y′≤0,∀x∈⇔{ay′<0Δy′≤0m.
Chú ý: khi hệ số achứa tham số thì cần xét thêm trường hợpa=0.
Bài toán 2: Tìm tham số m để hàm sốy=ax+bcx+d (c≠0,ad−bc≠0) đơn điệu trên mỗi khoảng xác định.
Phương pháp giải:
Tập xác định: D=R∖{−dc}.
Đạo hàm: y′=ad−bc(cx+d)2 .
Điều kiện đơn điệu:
Hàm số đồng biến trên từng khoảng xác định⇔y′>0,∀x∈D⇔ad−bc>0→m.
Hàm số nghịch biến trên từng khoảng xác định⇔y′<0,∀x∈D⇔ad−bc<0→m.
Bài toán 3: Tìm tham số m để hàm số đa thức đơn điệu trên tập K (với K là khoảng, đoạn hoặc nửa khoảng).
Phương pháp giải:
Bước 1: Tìm đạo hàm của hàm y′=f′(x).
Bước 2: Sử dụng điều kiện đơn điệu:
- Hàm số đồng biến trên K⇔y′≥0,∀x∈K.
- Hàm số nghịch biến trên K⇔y′≤0,∀x∈K.
Bước 3: Tìm tham số m
Loại 1: (nếu cô lập được m)
+ Biến đổi theo dạng h(m)≥g(x),∀x∈K (hoặc h(m)≤g(x),∀x∈K).
+ Lập bảng biến thiên của hàm số g(x) với mọi x∈K.
+ Dựa vào bảng biến thiên và kết luận điều kiện cho tham số m.
+ Chú ý: với các hàm đa thức việc xét đồng biến trên khoảng (a;b)⇔ xét đồng biến trên khoảng [a;b].
Loại 2: Không cô lập được tham số m; nhưng y′=0 có nghiệm đẹp
+ Tìm trực tiếp nghiệm của phương trình y′=0
+ Áp dụng điều kiện nghiệm của đề bài cho nghiệm của y′.
Loại 3: Không cô lập được tham số m vày′=0 không có nghiệm đẹp
+ Sử dụng trực tiếp cách xét dấu tam thức bậc 2 để xử lý
Bài tập tự luyện có đáp án
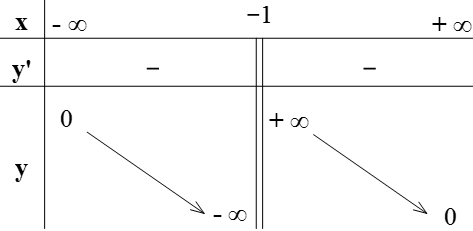
Câu 1: Cho hàm số y=f(x) có bảng biến thiên
 Khẳng định nào sau đây là đúng
Khẳng định nào sau đây là đúng
 Khẳng định nào sau đây là đúng
Khẳng định nào sau đây là đúng- A
- B
- C
- D
Do y′<0 trên các khoảng (−∞;−1),(−1;+∞) nên hàm số cũng nghịch biến trên các khoảng đó.
Câu 2: Hàm số y=−13x3+(m−2)x2−mx+3m nghịch biến trên khoảng xác định khi:
- A
- B
- C
- D
Ta có y′=−x2+2(m−2)x−m
Hàm số nghịch biến trên tập xác định khi và chỉ khi y′≤0,∀x∈R⇔−x2+2(m−2)x−m≤0,∀x∈R
⇔Δ′≤0⇔(m−2)2−m≤0⇔m2−5m+4≤0⇔1≤m≤4 .
Câu 3: Với giá trị nào của m, hàm số y=(m−2)x+mx+m đồng biến trên mỗi khoảng xác định của nó?
- A
- B
- C
- D
TXĐ: D=(−∞;−m)∪(−m;+∞) ; y′=m(m−2)−m(x+m)2=m2−3m(x+m)2
y đồng biến trên mỗi khoảng xác định ⇔y′>0⇔m2−3m>0⇔[m>3m<0
Câu 4: Cho hàm số y=ax+bcx+d(ad−bc≠0) . Chọn khẳng định đúng trong các khẳng đinh sau?
- A
- B
- C
- D
Ta có y′=ad−bc(cx+d)2⇒ Dấu của y′ sẽ phụ thuộc vào ad−bc⇒ Hàm số luôn đơn điệu trên các khoảng của tập xác định
Câu 5: Tìm m để hàm số y=13x3+mx2+4 đồng biến trên R ?
- A
- B
- C
- D
Ta có y′=x2+2mx
Hàm số đồng biến trên R ⇔y′≥0,∀x∈R⇔x2+2mx≥0,∀x∈R⇔Δ′≤0⇔m2≤0⇔m=0 .
Câu 6: Tìm GTNN của m để hàm số y=x33+mx2−mx−m đồng biến trên R ?
- A
- B
- C
- D
Ta có y′=x2+2mx−m
Hàm số đồng biến trên R⇔y′≥0,∀x∈R⇔x2+2mx−m≥0,∀x∈R⇔Δ′≤0⇔m2+m≤0 ⇔−1≤m≤0 .
Câu 7: Hàm số nào sau đây nghịch biến trên R với mọi m?
- A
- B
- C
- D
Hàm y=−m2x3+m loại ngay vì với m=0 thì y=0 .
Hàm y=−m2x3+mx2−3x+1 có y′=−3m2x2+2mx−3=−(mx√3−1√3)2−83<0,∀x∈R⇒y nghịch biến trên R với ∀m∈R .
Hàm y=−mx+1x+m loại ngay vì TXĐ của hàm số y=−mx+1x+m là R∖{−m} không phải R .
Hàm y=x3−2mx+1 có y′=3x2−2m , ta chưa thể khẳng định được với ∀m∈R thì y′≤0,∀x∈R⇒ Loại.
Câu 8: Hàm số y=x33+mx2+4x đồng biến trên R khi?
- A
- B
- C
- D
Yêu cầu bài toán
⇔y′=x2+2mx+4⩾0,∀x∈R⇔{a=1>0Δ′=m2−4⩽0⇔m2⩽4⇔−2⩽m⩽2
Câu 9: Hàm số y=−x33+mx2−4x nghịch biến trên R khi:
- A
- B
- C
- D
Yêu cầu bài toán
⇔y′=−x2+2mx−4⩽0,∀x∈R⇔{a=−1<0Δ′=m2−4⩽0⇔m2⩽4⇔−2⩽m⩽2.
Câu 10: Tất cả các giá trị của m để hàm số f(x)=x−mx−1 nghịch biến trên từng khoảng xác định của nó là:
- A
- B
- C
- D
TXĐ: (−∞;1)∪(1;+∞);f′(x)=m−1(x−1)2 .
f(x) nghịch biến trên từng khoảng xác định ⇔y′<0⇔m−1<0⇔m<1 .
Câu 11: Cho hàm số y=3x+1x−3. Khẳng định nào sau đây là đúng?
- A
- B
- C
- D
TXĐ: D=R∖{3}
Ta có y′=−10(x−3)2<0∀x∈D⇒Hàm số luôn nghịch biến trên các khoảng xác định.
Câu 12: Cho hàm số f(x) đồng biến trên tập số thực R , mệnh đề nào sau đây là đúng?
- A
- B
- C
- D
Theo định nghĩa hàm số đồng biến SGK lớp 10.
Câu 13: Tất cả các giá trị của m để hàm số y=−x3+mx nghịch biến trên R là:
- A
- B
- C
- D
y′=−3x2+m;y′≤0∀x⇔m≤0
Xem thêm các bài tiếp theo bên dưới