Quãng đường đi được, vận tốc tức thời của một vật
Lưu về Facebook:
Lý thuyết về Quãng đường đi được, vận tốc tức thời của một vật
Giả sử một vật chuyển động với vận tốc thay đổi theo thời gian biểu thị bởi công thức $v = v(t) (0 \le t \le T)$. Quãng đường $L$ vật đi được từ thời điểm $t = a$ tới thời điểm $t = b$ $(0 \le a \le b \le T)$ là: $$L = \int\limits_{a}^{b} {v(t)dt}.$$
Nếu vật chuyển động có gia tốc thay đổi theo thời gian biểu thị bởi công thức $a = a(t) (0 \le t \le T)$. Vận tốc ở thời điểm $t_0$ là $v_0$, vận tốc ở thời điểm $t_1$ được tính bởi công thức: $$v_1 = \int\limits_{t_0}^{t_1} {a(t)dt} + v_0.$$
Trong chuyển động biến đổi đều ta luôn có: $\left\{ \begin{array}{l} v = s'\\ a = v'\end{array}\right.$
Bài tập tự luyện có đáp án
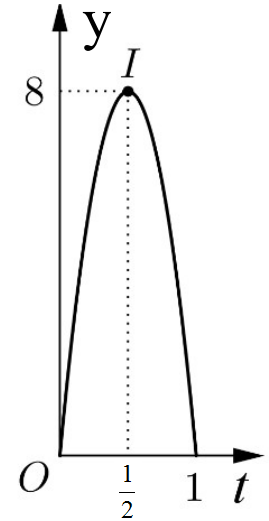
Câu 1:  Một người chạy trong thời gian 1 giờ, vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol với đỉnh $I\left( \dfrac{1}{2};8 \right)$ và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s người đó chạy được trong khoảng thời gian 45 phút, kể từ khi bắt đầu chạy.
Một người chạy trong thời gian 1 giờ, vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol với đỉnh $I\left( \dfrac{1}{2};8 \right)$ và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s người đó chạy được trong khoảng thời gian 45 phút, kể từ khi bắt đầu chạy.
 Một người chạy trong thời gian 1 giờ, vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol với đỉnh $I\left( \dfrac{1}{2};8 \right)$ và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s người đó chạy được trong khoảng thời gian 45 phút, kể từ khi bắt đầu chạy.
Một người chạy trong thời gian 1 giờ, vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol với đỉnh $I\left( \dfrac{1}{2};8 \right)$ và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s người đó chạy được trong khoảng thời gian 45 phút, kể từ khi bắt đầu chạy.- A
- B
- C
- D
Theo bài ra ta có : $v\left( t \right)=-32{{t}^{2}}+32t$. Vậy $s=\int\limits_{0}^{\dfrac{3}{4}}{\left( -32{{t}^{2}}+32t \right)}dt=4,5km$