Vị trí tương đối giữa mặt phẳng và mặt cầu
Lý thuyết về Vị trí tương đối giữa mặt phẳng và mặt cầu
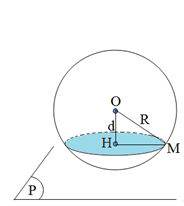
Cho mặt cầu S(O;R) và mặt phẳng (P). Gọi H là hình chiếu của O trên mặt phẳng (P) và đặt d=d(O;(P))=OH. Khi đó:
- Nếu d<R thì thì mp(P) cắt mặt cầu S(O:R) theo giao tuyến là đường tròn nằm trên mp(P) có tâm là H và bán kính r=√R2−d2.
Khi d=0 thì mp(P) đi qua tâm O của mặt cầu, mặt phẳng đó được gọi là mặt phẳng kính, giao tuyến của mặt phẳng kính với mặt cầu là đường tròn có bán kính R gọi là đường tròn lớn của mặt cầu
- Nếu d=R thì mp(P) cắt mặt cầu tại một điểm duy nhất H.
Khi đó ta nói mặt phẳng (P) tiếp xúc với mặt cầu S(O;R) tại điểm H hoặc còn nói mp(P) là tiếp diện của mặt cầu tại điểm H, điểm H gọi là điểm tiếp xúc ( hoặc tiếp điểm ) của (P) và mặt cầu.
- Nếu d>R thì mp(P) không cắt mặt cầu S(O;R)
Bài tập tự luyện có đáp án
Câu 1: Cho mặt cầu (S) có tâm I, bán kính R=2 và mặt phẳng (P) . Trong các khẳng định sau, khẳng định sai là
- A
- B
- C
- D
Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn nếu d(I,(P))<2
Suy ra, khẳng định ” Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường thẳng nếu d(I,(P))<2 “ sai.
Câu 2: Cho điểm M nằm trong mặt cầu (S). Mặt phẳng đi qua điểm M cắt mặt cầu theo giao tuyến là
- A
- B
- C
- D
Vì điểm M nằm trong mặt cầu (S) nên mặt phẳng đi qua điểm M cắt mặt cầu theo giao tuyến là đường tròn.