Các đoạn mạch vuông pha
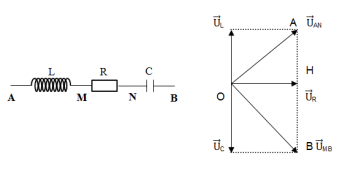
Lý thuyết về Các đoạn mạch vuông pha
Khi ${{U}_{RL}}\bot {{U}_{RC}}$ ta có: $\dfrac{{{Z}_{L}}}{R}.\dfrac{{{Z}_{C}}}{R}=1\Leftrightarrow {{Z}_{L}}.{{Z}_{C}}={{R}^{2}}$
Áp dụng hệ thức lượng trong tam giác vuông ta có: $\dfrac{1}{U_{R}^{2}}=\dfrac{1}{U_{RL}^{2}}+\dfrac{1}{U_{RC}^{2}}$
Trog đó: $R$ , $Z_L$ , $Z_C$ là điện trở, cảm kháng và dung kháng của mạch.
$U_R$ , $U_{RL}$ , $U_{RC}$ là điện áp hiệu dụng 2 đầu điện trở, điện trở và cuộn cảm, điện trở và tụ điện.
Đối với các đoạn mạch vuông pha khác ta áp dụng tương tự.
Bài tập tự luyện có đáp án
Câu 1: Mạch điện RCL nối tiếp có C thay đổi được. Điện áp hai đầu đoạn mạch $u=150\sqrt{2}\cos 100\pi t$(V). Khi $C={{C}_{1}}=\dfrac{62,5}{\pi }\mu F$ thì mạch tiêu thụ công suất cực đại $P_{max} = 93,75 W$. Khi $C={{C}_{2}}=\dfrac{1}{9\pi }mF$ thì điện áp hai đầu đoạn mạch RC và cuộn dây vuông pha với nhau, điện áp hiệu dụng hai đầu cuộn dây khi đó là
- A
- B
- C
- D
+ Khi $C={{C}_{1}}=\dfrac{62,5}{\pi }\mu F$ thì mạch tiêu thụ công suất cực đại Pmax = 93,75 W, lúc này mạch đang xảy ra cộng hưởng $\Rightarrow {{Z}_{L}}={{Z}_{{{C}_{1}}}}=160\Omega $
${{P}_{\max }}=93,75=\dfrac{{{U}^{2}}}{R+r}\Rightarrow R+r=240\Omega $
+ Khi $C={{C}_{2}}=\frac{1}{9\pi }mF\Rightarrow {{Z}_{{{C}_{2}}}}=90\Omega $ thì điện áp hai đầu đoạn mạch RC và cuộn dây vuông pha với nhau nên cuộn dây có điện trở r.
Ta có: $\dfrac{{{Z}_{L}}}{r}.\dfrac{{{Z}_{C}}}{R}=1\Rightarrow \dfrac{160}{r}.\dfrac{90}{240-r}=1\Rightarrow r=120\Omega; R=120\Omega. $
Điện áp 2 đầu cuộn dây:
${{U}_{d}}=\dfrac{U.\sqrt{Z_{L}^{2}+{{r}^{2}}}}{\sqrt{{{\left( R+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=120V$