Số cực đại, cực tiểu giữa 2 nguồn cùng pha
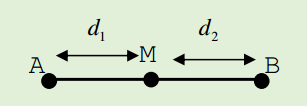
Lý thuyết về Số cực đại, cực tiểu giữa 2 nguồn cùng pha
Phương trình giao thoa sóng tại M: ${{u}_{M}}={{u}_{1M}}+{{u}_{2M}}$
${{u}_{M}}=2Ac\text{os}\left[ \pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\dfrac{\Delta \varphi }{2} \right]c\text{os}\left[ 2\pi ft-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda }+\dfrac{{{\varphi }_{1}}+{{\varphi }_{2}}}{2} \right]$
Biên độ dao động tại M: ${{A}_{M}}=2A\left| c\text{os}\left( \pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\dfrac{\Delta \varphi }{2} \right) \right|$ với $\Delta \varphi =\left| {{\varphi }_{1}}-{{\varphi }_{2}} \right|$
Biên độ phụ thuộc vào hiệu đường truyền và độ lệch pha.
2 nguồn cùng pha: ${{u}_{M}}=2Ac\text{os}\left[ \pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda } \right]c\text{os}\left[ 2\pi ft-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda }\right]$
Trung trực là cực đại giao thoa
$AB=\ell $
M dao động với biên độ cực đại: ${{A}_{\max }}=2A\Leftrightarrow \cos \left( \frac{\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right) \right)=\pm 1\Leftrightarrow \frac{\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right)=k\pi \Rightarrow {{d}_{2}}-{{d}_{1}}=k\lambda $
Mà ${{d}_{1}}+{{d}_{2}}=AB$ $\Rightarrow {{d}_{2}}=\dfrac{AB}{2}+\dfrac{k\lambda }{2}$
Mặt khác: $M\in \ell \Rightarrow 0<{{d}_{2}}<\ell \Rightarrow \dfrac{-\ell }{\lambda }
M dao động với biên độ cực tiểu ( không dao động):${{A}_{\min }}=0\Leftrightarrow \cos \left( \dfrac{\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right) \right)=0\Leftrightarrow \dfrac{\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right)=\dfrac{\pi }{2}+k\pi \Rightarrow {{d}_{2}}-{{d}_{1}}=\left( 2k+1 \right)\dfrac{\lambda }{2}$
Mà ${{d}_{1}}+{{d}_{2}}=\ell$$\Rightarrow {{d}_{2}}=\dfrac{\ell }{2}+\left( 2k+1 \right)\dfrac{\lambda }{4}$
Mặt khác: $M\in \ell \Rightarrow 0<{{d}_{2}}<\ell \Rightarrow \dfrac{-\ell }{\lambda }-\dfrac{1}{2}
2 cực đại hoặc 2 cực tiểu liên tiếp cách nhau $\frac{\lambda }{2}$
1 cực đại và 1 cực tiểu liên tiếp cách nhau $\frac{\lambda }{4}$
Bài tập tự luyện có đáp án
Câu 1: Ở mặt thoáng của một chất lỏng, tại hai điểm A và B cách nhau 20 cm có hai nguồn sóng dao động điều hòa theo phương thẳng đứng, cùng pha, cùng biên độ và cùng tần số 50 Hz. Coi biên độ sóng không đổi khi sóng truyền đi. Tốc độ truyền sóng trên mặt chất lỏng là 3 m/s. Trên đoạn thẳng AB, số điểm dao động có biên độ cực đại là
- A
- B
- C
- D
$\begin{align}& \lambda =\dfrac{v}{f}=6\left( cm \right) \\ & \dfrac{-AB}{\lambda }<k<\dfrac{AB}{\lambda }\Leftrightarrow -3,33<k<3,33 \\ \end{align}$
Có 7 giá trị k thỏa mãn.
Câu 2: Ở mặt nước có hai nguồn sóng dao động theo phương vuông góc với mặt nước, có cùng phương trình u = Acos\(\omega \)t. Trong miền gặp nhau của hai sóng, những điểm mà ở đó các phần tử nước dao động với biên độ cực đại sẽ có hiệu đường đi của sóng từ hai nguồn đến đó bằng
- A
- B
- C
- D
Các phần tử nước dao động với biên độ cực đại sẽ có hiệu đường đi của sóng từ hai nguồn đến đó bằng một số nguyên lần bước sóng.
Câu 3: Ở mặt nước có hai nguồn sóng dao động theo phương vuông góc với mặt nước, có cùng phương trình u = Acos\(\omega \)t. Trong miền gặp nhau của hai sóng, những điểm mà ở đó các phần tử nước dao động với biên độ cực tiểu sẽ có hiệu đường đi của sóng từ hai nguồn đến đó bằng
- A
- B
- C
- D
Các phần tử nước dao động với biên độ cực tiểu sẽ có hiệu đường đi của sóng từ hai nguồn đến đó bằng một số lẻ lần nửa bước sóng.
Câu 4: (CĐ-2014): Trong thí nghiệm về giao thoa sóng nước, hai nguồn A và B cách nhau 16 cm, dao động điều hòa theo phương vuông góc mặt nước với cùng phương trình u = 2cos16\(\pi \)t (u tính bằng mm, t tính bằng s). Tốc độ truyền sóng trên mặt nước là 12 cm/s. Trên đoạn AB, số điểm dao động với biên độ cực đại là:
- A
- B
- C
- D
$f=\dfrac{\omega }{2\pi }=\dfrac{16\pi }{2\pi }=8\left( Hz \right)$
$\begin{align}& \lambda =\dfrac{v}{f}=1,5\left( cm \right) \\ & \dfrac{-AB}{\lambda }<k<\dfrac{AB}{\lambda }\Leftrightarrow -10,67<k<10,67 \\ \end{align}$
Có 21 giá trị k thỏa mãn.
Câu 5: (CĐ-2013): Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp dao động cùng pha được đặt tại A và B cách nhau 18 cm. Sóng truyền trên mặt nước với bước sóng 3,5 cm. Trên đoạn AB, số điểm mà tại đó phần tử nước dao động với biên độ cực đại là
- A
- B
- C
- D
$\dfrac{-AB}{\lambda }<k<\dfrac{AB}{\lambda }\Leftrightarrow -5,14<k<5,14$
Có 11 giá trị k thỏa mãn.
Câu 6: Để khảo sát giao thoa sóng cơ, người ta bố trí trên mặt nước nằm ngang hai nguồn kết hợp $S_{1}$ và $S_{2}$. Hai nguồn này dao động điều hòa theo phương thẳng đứng, cùng pha. Xem biên độ sóng không thay đổi trong quá trình truyền sóng. Các điểm thuộc mặt nước và nằm trên đường trung trực của đoạn $S_{1}$ $S_{2}$ sẽ
- A
- B
- C
- D
Khi hai nguồn sóng là hai nguồn kết hợp và cùng pha nhau thì các điểm thuộc mặt nước và nằm trên đường trung trực của đoạn S1S2 sẽ dao động với biên độ cực đại.
Câu 7: (ĐH-2013): Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp dao động cùng pha đặt tại hai điểm A và B cách nhau 16cm. Sóng truyền trên mặt nước với bước sóng 3cm. Trên đoạn AB, số điểm mà tại đó phần tử nước dao động với biên độ cực đại là:
- A
- B
- C
- D
$\dfrac{-AB}{\lambda }<k<\dfrac{AB}{\lambda }\Leftrightarrow -5,33<k<5,33$
Có 11 giá trị k thỏa mãn.
Câu 8: Trên mặt chất lỏng có hai nguồn sóng kết hợp A và B cùng biên độ cùng pha cách nhau 10 cm. Hai điểm nguồn A và B gần như đứng yên (coi như cực tiểu dao động) và giữa chúng còn 10 điểm đứng yên không dao động. Biết tần số rung là 26 Hz, tính tốc độ truyền sóng
- A
- B
- C
- D
Vì giữa AB có 10 điểm đứng yên không dao động nên ta có:
$AB=11\dfrac{\lambda }{2}=10\left( cm \right)\Rightarrow \lambda =\dfrac{20}{11}\left( cm \right)\Rightarrow v=\lambda .f\approx 0,47\left( m/s \right)$
Câu 9: Chọn câu đúng. Thực hiện thí nghiệm giao thoa trên mặt nước: A và B là hai nguồn kết hợp có phương trình sóng tại A, B là: uA = uB = a.cosωt thì quỹ tích những điểm dao động với biên độ cực đại bằng 2a là:
- A
- B
- C
- D
Xem lại bài giao thoa, chú ý phần sự tạo thành các vân giao thoa. Nhớ lại định nghĩa hypecbon: quĩ tích của những điểm có hiệu khoảng cách đến 2 điểm cố định là không đổi. Hai điểm cố định được gọi là các tiêu điểm của hypecbon.
Xem thêm các bài tiếp theo bên dưới