Điểm giao thoa có khoảng cách cực đại, cực tiểu
Lưu về Facebook:
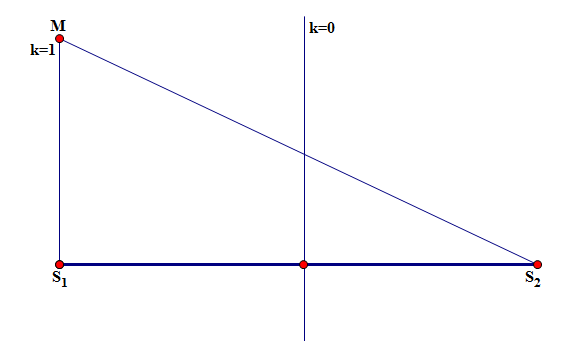
Lý thuyết về Điểm giao thoa có khoảng cách cực đại, cực tiểu
M thuộc đường thẳng vuông với đường nối 2 nguồn tại 1 trong 2 nguồn
Khoảng cách từ M đến đường thẳng nối 2 nguồn lớn nhất khi M thuộc đường cực đại thứ nhất (k=1)
M gần đường thẳng nối 2 nguồn nhất thì M phải thuộc đường cực đại có k lớn nhất
Nếu M thuộc đoạn AB thì để AM (BM) nhỏ nhất thì k cũng phải có giá trị lớn nhất.
MS2−MS1=λ;MS22=MS21+S1S22(MS1=dmax)
MS2−MS1=kmaxλ;MS22=MS21+S1S22 (MS1=dmin)
Bài tập tự luyện có đáp án
Câu 1: Trên mặt nước nằm ngang có hai nguồn kết hợp S1 và S2 dao động theo phương thẳng đứng, cùng pha, với cùng biên độ a, xem biên độ không đổi trong qua trình truyền sóng. Khi có sự giao thoa hai sóng đó trên mặt nước thì dao động của phần tử nước tại trung điểm của đoạn S1S2 có biên độ bằng
- A
- B
- C
- D
Với hai nguồn cùng pha thì trung điểm của S1S2 dao động với biên độ cực đại
Xem thêm các bài tiếp theo bên dưới