Phương trình dạng chứ dấu | |, chứa ẩn ở mẫu

$ |2x-1|\,=\,|x+2|\Leftrightarrow \left[ \begin{array}{l} & 2x-1=x+2 \\ & 2x-1=-x-2 \end{array} \right.\Leftrightarrow \left[ \begin{array}{l} & x=3 \\ & x=-\dfrac{1}{3} \end{array} \right.. $

Điều kiện: $ x-1\ge 0\Leftrightarrow x\ge 1. $

Điều kiện: $ \left\{ \begin{array}{l} & 1-x\ge 0 \\ & x+2\ne 0 \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & x\le 1 \\ & x\ne -2 \end{array} \right.. $

Điều kiện: $ x\ge 2 $ .

Khi đó: $ \sqrt{x-2}+x=\sqrt{x-2}+3\Leftrightarrow x=3. $

Điều kiện $ x\ne 0 $ .

Phương trình  $ \dfrac{2x-1}{x}=1\Leftrightarrow 2x-1=x\Leftrightarrow x=1$(Thỏa mãn).

Vậy nghiệm của phương trình là $x = 1$.

Điều kiện: $ \left\{ \begin{array}{l} & x-2\ge 0 \\ & 2-x\ge 0 \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & x\ge 2 \\ & x\le 2 \end{array} \right.\Leftrightarrow x=2. $

Với $ x=2 $ thay vào ta thấy $ 2=1 $ (vô lý)

Vậy phương trình vô nghiệm.

Thay lần lượt các giá trị $ x=1 ;x=2; x=-1;x=3 $ ta thấy giá trị $ x=2 $ thỏa mãn phương trình đã cho.

Do đó $ x=2 $ là một nghiệm của phương trình.

Điều kiện: $ x-1\ne 0\Leftrightarrow x\ne 1. $

$ \dfrac{m{{x}^{2}}}{|x|-1}=m|x|+2m+1 $ (1)

Điều kiện: $ |x|\ne 1 $

Khi đó từ phương trình (1) suy ra

$ \begin{array}{l} & m{{x}^{2}}=\left( m|x|+2m+1 \right)\left( |x|-1 \right) \\ & \Leftrightarrow (m+1)|x|=2m+1\,\,\,\,\,\,\,\,\,\,\,\,(2) \end{array} $

+) Trường hợp 1: $ m=-1 $

$ \Rightarrow \,\,\,(2)\Leftrightarrow 0|x|=-1 $ (vô lý)

+) Trường hợp 2: $ m\ne -1 $

$ \Rightarrow \,\,(2)\Leftrightarrow |x|=\dfrac{2m+1}{m+1} $ (3)

Ta có: $ |x|\ne 1\,\Leftrightarrow \dfrac{2m+1}{m+1}\ne 1\Leftrightarrow \dfrac{m}{m+1}\ne 0\Leftrightarrow \left\{ \begin{array}{l} & m\ne -1 \\ & m\ne 0 \end{array} \right.. $

Nếu $ m=-\dfrac{1}{2} $ thì phương trình (3) có nghiệm duy nhất $ x=0 $ .

Nếu $ \dfrac{2m+1}{m+1} < 0\Leftrightarrow -1 < m < -\dfrac{1}{2} $ $ \Rightarrow \, $ (3) vô nghiệm.

Nếu $ \dfrac{2m+1}{m+1} > 0\Leftrightarrow \left[ \begin{array}{l} & m > -\dfrac{1}{2} \\ & m < -1 \end{array} \right. $

$ \Rightarrow $ Phương trình (3) có 2 nghiệm phân biệt $ x=\pm \dfrac{2m+1}{m+1} $

Vậy $ m\in \left( -\infty ;\,-1 \right)\cup \left( -\dfrac{1}{2};+\infty \right)\backslash \left\{ 0\, \right\} $ phương trình có 2 nghiệm phân biệt $ x=\pm \dfrac{2m+1}{m+1} $

$ \begin{array}{l} & \sqrt{{{x}^{2}}-x+1-3{{m}^{2}}}=x-m \\ & \Leftrightarrow \left\{ \begin{array}{l} & x\ge m \\ & {{x}^{2}}-x+1-3{{m}^{2}}={{(x-m)}^{2}} \end{array} \right. \\ & \Leftrightarrow \left\{ \begin{array}{l} & x\ge m \\ & (2m-1)x=4{{m}^{2}}-1\,\,\,(1) \end{array} \right. \end{array} $

Với $ m=\dfrac{1}{2} $ thì $ (1)\Leftrightarrow 0x=0 $ (luôn đúng) $ \Rightarrow $ (1) có vô số nghiệm.

Với $ m\ne \dfrac{1}{2} $ thì (1) có nghiệm duy nhất $ x=2m+1 $

Ta có: $ x=2m+1\ge m\Leftrightarrow m\ge -1 $

Vậy với $ m\ge -1\,;\,m\ne \dfrac{1}{2} $ thì phương trình có nghiệm duy nhất $ x=2m+1 $ .

$ \dfrac{{{x}^{2}}-4}{{{(x-2)}^{2}}}=\dfrac{x+1}{x-m} $ (1).

Điều kiện: $ x\ne 2\,;\,x\ne m $ .

Khi đó:

$ \begin{array}{l} & \dfrac{x+2}{x-2}=\dfrac{x+1}{x-m} \\ & \Leftrightarrow (x+2)(x-m)=(x+1)(x-2) \\ & \Leftrightarrow x(3-m)=2m-2\,\,\,\,\,(2) \end{array} $

Với $ m=3 $ thay vào (2) ta được: $ 0x=4 $ (vô lý).

Với $ m\ne 3 $ $ \Rightarrow $ Phương trình (2) có nghiệm duy nhất $ x=\dfrac{2m-2}{3-m} $

$ x\ne 2\Leftrightarrow \dfrac{2m-2}{3-m}\ne 2\Leftrightarrow \left\{ \begin{array}{l} & m\ne 2 \\ & m\ne 3 \end{array} \right. $ .

$ x\ne m\Leftrightarrow \dfrac{2m-2}{3-m}\ne m\Leftrightarrow \dfrac{{{m}^{2}}-m-2}{3-m}\ne 0\Leftrightarrow \left\{ \begin{array}{l} & m\ne -1 \\ & m\ne 2 \\ & m\ne 3 \end{array} \right. $ .

Do đó với $ m\ne -1;,m\ne 2\,;\,m\ne 3 $ thì phương trình có nghiệm duy nhất $ x=\dfrac{2m-2}{3-m} $ .

$ x < -2\Leftrightarrow \dfrac{2m-2}{3-m} < -2\Leftrightarrow \dfrac{4}{3-m} < 0\Leftrightarrow m > 3 $

Vậy $ m\in (3;+\infty ) $ thỏa mãn đề bài.

$ \begin{array}{l} & \sqrt{4{{x}^{2}}-4mx+{{m}^{2}}}=2-x \\ & \Leftrightarrow \sqrt{{{(2x-m)}^{2}}}=2-x \\ & \Leftrightarrow |2x-m|\,=2-x \\ & \Leftrightarrow \left[ \begin{matrix} \left\{ \begin{array}{l} & x\le 2 \\ & 2x-m=2-x \end{array} \right. \\ \left\{ \begin{array}{l} & x\le 2 \\ & 2x-m=x-2 \end{array} \right. \\ \end{matrix} \right.\Leftrightarrow \left[ \begin{array}{l} & \left\{ \begin{array}{l} & x\le 2 \\ & x=\dfrac{m+2}{3} \end{array} \right. \\ & \left\{ \begin{array}{l} & x\le 2 \\ & x=m-2 \end{array} \right. \end{array} \right. \end{array} $

+) $ x=\dfrac{m+2}{3}\le 2\Leftrightarrow m\le 4 $

+) $ x=m-2\le 2\Leftrightarrow m\le 4 $

Vậy $ m\le 4 $ phương trình có nghiệm: $ x=\dfrac{m+2}{3}\,;\,x=m-2 $ .

$ \sqrt{x-2\sqrt{x-1}}+\sqrt{x+3-4\sqrt{x-1}}=m $ (1)

Điều kiện: $ x\ge 1 $ .

$ \begin{array}{l} & (1)\Leftrightarrow \sqrt{{{\left( \sqrt{x-1}-1 \right)}^{2}}}+\sqrt{{{\left( \sqrt{x-1}-2 \right)}^{2}}}=m \\ & \Leftrightarrow \left| \sqrt{x-1}-1 \right|+\left| \sqrt{x-1}-2 \right|=m \end{array} $

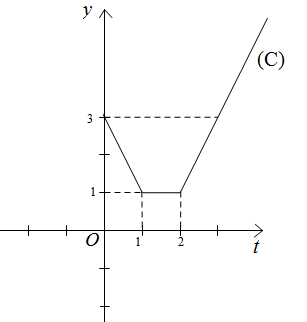
Đặt $ t=\sqrt{x-1}\,\,\,(t\ge 0) $ ta có phương trình: $ |t-1|+|t-2|=m $ (2)

Vẽ đồ thị hàm số: $ y=f(t)=|t-1|+|t-2|\,\,\, $ (C) với $ t\ge 0 $.

Ta có: $ f(t)=\left\{ \begin{array}{lll} 2t-3 & khi & t > 2 \\ 1\ & khi\ & 1\le t\le 2 \\ 3-2t & khi & 0\le t < 1 \end{array} \right. $

Số nghiệm của phương trình (2) là số giao điểm của đồ thị hàm số (C) với đường thẳng $ y=m $ .

Do đó, để phương trình có 2 nghiệm phân biệt thì $ 1 < m\le 3 $ .

$ |1-x|+|x|=m-1 $ (1)

Ta thấy nếu $ {{x}_{0}} $ là nghiệm của (1) thì $ (1-{{x}_{0}}) $ cũng là nghiệm của (1).

Do đó (1) có nghiệm duy nhất $ \Leftrightarrow {{x}_{0}}=1-{{x}_{0}}\Leftrightarrow {{x}_{0}}=\dfrac{1}{2}. $

Thay $ {{x}_{0}}=\dfrac{1}{2} $ vào (1) ta được: $ m-1=1\Leftrightarrow m=2. $

Với $ m=2 $ phương trình (1) trở thành: $ |1-x|+|x|=1 $ (2)

Giải phương trình (2) ta có tập nghiệm $S = {\rm{ }}\left\{ {0;1} \right\}$ .

Vậy không có giá trị nào của $ m $ để phương trình có nghiệm duy nhất.

$ \dfrac{2mx-m}{\sqrt{x-1}}+\sqrt{x-1}=\dfrac{2(x+m)-1}{\sqrt{x-1}} $ (1)

Điều kiện: $ x > 1 $

Từ phương trình (1) suy ra:

$ \begin{array}{l} & 2mx-m+x-1=2x+2m-1 \\ & \Leftrightarrow (2m-1)x=3m\,\,\,\,\,\,\,\,\,\,(2) \end{array} $

Với $ m=\dfrac{1}{2} $ $ \Rightarrow \,\,\,(2)\Leftrightarrow 0x=\dfrac{3}{2} $ (vô lý)

Với $ m\ne \dfrac{1}{2}\,\, $ $ \Rightarrow $ (2) có nghiệm duy nhất $ x=\dfrac{3m}{2m-1} $

Để phương trình đã cho có nghiệm thỏa mãn $ x < 2 $ thì

$ 1 < \dfrac{3m}{2m-1} < 2\Leftrightarrow \left\{ \begin{array}{l} & \dfrac{m+1}{2m-1} > 0 \\ & \dfrac{2-m}{2m-1} < 0 \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & \left[ \begin{array}{l} & m > \dfrac{1}{2} \\ & m < -1 \end{array} \right. \\ & \left[ \begin{array}{l} & m > 2 \\ & m < \dfrac{1}{2} \end{array} \right. \end{array} \right.\Leftrightarrow \left[ \begin{array}{l} & m < -1 \\ & m > 2 \end{array} \right. $ .

$ \begin{array}{l} & 4x+|2x-m|=2+3x\Leftrightarrow |2x-m|=2-x \\ & \Leftrightarrow \left[ \begin{array}{l} & \left\{ \begin{array}{l} & 2-x\ge 0 \\ & 2x-m=2-x \end{array} \right. \\ & \left\{ \begin{array}{l} & 2-x\ge 0 \\ & 2x-m=x-2 \end{array} \right. \end{array} \right.\Leftrightarrow \left[ \begin{array}{l} & \left\{ \begin{array}{l} & x\le 2 \\ & x=\dfrac{m+2}{3} \end{array} \right. \\ & \left\{ \begin{array}{l} & x\le 2 \\ & x=m-2 \end{array} \right. \end{array} \right. \end{array} $

+) $ \dfrac{m+2}{3}\le 2\Leftrightarrow m\le 4. $

+) $ m-2\le 2\Leftrightarrow m\le 4. $

Vậy $ m\le 4 $ phương trình có nghiệm: $ x=\dfrac{m+2}{3}\,;\,x=m-2 $ .

$ m > 4 $ phương trình vô nghiệm.

$ \begin{array}{l} & |mx-2|=|x+2m| \\ & \Leftrightarrow \left[ \begin{array}{l} & mx-2=x+2m \\ & mx-2=-x-2m \end{array} \right. \\ & \Leftrightarrow \left[ \begin{array}{l} & (m-1)x=2m+2\,\,\,(1) \\ & (m+1)x=2-2m\,\,\,\,(2) \end{array} \right. \end{array} $

+) Xét phương trình (1).

Với $ m=1\,\,\Rightarrow \,\,0x=4 $ (vô lý) $ \Rightarrow $ (1) vô nghiệm.

Với $ m\ne 1\,\,\,\Rightarrow $ (1) có nghiệm $ x=\dfrac{2m+2}{m-1} $ .

+) Xét phương trình (2).

Với $ m=-1\,\,\Rightarrow \,\,0x=4 $ (vô lý) $ \Rightarrow $ (2) vô nghiệm.

Với $ m\ne -1\,\,\,\Rightarrow $ (2) có nghiệm $ x=\dfrac{2-2m}{m+1} $ .

Ta thấy $ m=1\,\,\Rightarrow $ (2) có nghiệm $ x=0 $

$ m=-1\,\,\Rightarrow $ (1) có nghiệm $ x=0 $

Vậy $ m\ne \pm 1 $ $ \Rightarrow $ Phương trình đã cho có 2 nghiệm $ {{x}_{1}}=\dfrac{2m+2}{m-1}\,;\,{{x}_{2}}=\dfrac{2-2m}{m+1} $ .

$ m=1\,\,\Rightarrow $ Phương trình có nghiệm $ x=0 $ .

$ m=-1\,\,\Rightarrow $ Phương trình có nghiệm $ x=0 $ .

$ \dfrac{{{x}^{2}}+(m-1)x-1}{\sqrt{x-2}}=\sqrt{x-2}\left( x-{{m}^{2}} \right) $ (1)

Điều kiện: $ x > 2 $

Khi đó từ phương trình (1) suy ra

$ \begin{array}{l} & {{x}^{2}}+(m-1)x-1=(x-2)(x-{{m}^{2}}) \\ & \Leftrightarrow {{x}^{2}}+(m-1)x-1={{x}^{2}}-{{m}^{2}}x-2x+2{{m}^{2}} \\ & \Leftrightarrow \left( {{m}^{2}}+m+1 \right)x=2{{m}^{2}}+1 \\ & \Leftrightarrow x=\dfrac{2{{m}^{2}}+1}{{{m}^{2}}+m+1} \end{array} $

$ \begin{array}{l} & x > 2\Leftrightarrow \dfrac{2{{m}^{2}}+1}{{{m}^{2}}+m+1} > 2 \\ & \Leftrightarrow \dfrac{-2m-1}{{{m}^{2}}+m+1} > 0 \\ & \Leftrightarrow -2m-1 > 0 \\ & \Leftrightarrow m < -\dfrac{1}{2} \end{array} $