Hình dạng của elip
Lý thuyết về Hình dạng của elip
Hình dạng của elip
a, Tâm đối xứng của elip:
Elip có phương trình (1) nhận các trục toạ độ làm các trục đối xứng và gốc toạ dộ là tâm đối xứng
b, Hình chữ nhật cơ sở
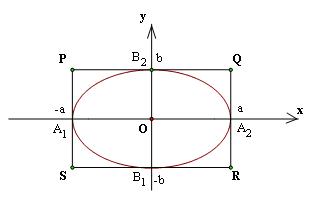
Vẽ qua $A1$&$A2$ hai đường thẳng song song với trục tung, vẽ qua $B1&B2$ hai đường thẳng song song với trục hoành. Bốn đường thẳng đó tạo thành hình chữ nhật $PQRS$. Ta gọi hình chữ nhật đó là hình chữ nhật cơ sở của elip
Từ đó suy ra
Mọi điểm của elip nếu không phải là đỉnh đều nằm trong hình chữ nhật cơ sở của nó, bốn đỉnh của elip là trung điểm các cạnh của hình chữ nhật cơ sở
c) Tâm sai của elip
Tỉ số giữa tiêu cự và độ dài trục lớn của elip goi là tâm sai của elip và được kí hiệu là e tức là $e=\dfrac{c}{a}$.
- Nếu tâm sai e càng bé (tức là càng gần 0) thì b càng gần a và hình chữ nhật cơ sở càng gần với hình vuông, do đó đường elip càng “béo”
- Nếu tâm sai e càng lớn (tức là càng gần1) thì tỉ số $\dfrac{b}{a}$càng gần tới 1 và hình chữ nhật cơ sở càng “dẹt”, do đó đường elip càng “gầy”
d) Elip và phép co đường tròn
Trong mặt phẳng tọa độ, cho đường tròn $(C)$ có phương trình${{x}^{2}}+{{y}^{2}}=a$và 1 số $k(0<k<1)$. Với mỗi điểm $M(x;y)$ trên $(C)$ lấy điểm $M′(x′;y′)$ sao cho $x′=x,y′=ky$ . Khi đó, tập hợp các điểm $M’$ là elip $(E)$ có phương trình chính tắc:
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Người ta nói: Phép co về trục hoành theo hệ số k biến đường tròn (C ) thành elip (E)
Bài tập tự luyện có đáp án
Câu 1: Elip $ \dfrac{{{x}^{\text{2}}}}{20}\text{+}\dfrac{{{y}^{\text{2}}}}{\text{12}}=1 $ có tiêu cự là:
- A
- B
- C
- D
Từ dạng của elip $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ ta có $ \left\{ \begin{array}{l} & a=2\sqrt{5} \\ & b=2\sqrt{3} \end{array} \right. $ .
Từ công thức $ {{b}^{2}}={{a}^{2}}-{{c}^{2}}\Rightarrow c=2\sqrt{2}\Rightarrow {{F}_{1}}{{F}_{2}}=2c=4\sqrt{2} $ .
Câu 2: Elip $ \dfrac{{{x}^{\text{2}}}}{\text{25}}\text{+}\dfrac{{{y}^{\text{2}}}}{20}=1 $ có phương trình đường chuẩn là:
- A
- B
- C
- D
Từ dạng của elip $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ ta có $ \left\{ \begin{array}{l} & a=5 \\ & b=2\sqrt{5} \end{array} \right. $ .
Từ công thức $ {{b}^{2}}={{a}^{2}}-{{c}^{2}}\Rightarrow c=\sqrt{5} $ .
Tâm sai của elip $ e=\dfrac{c}{a}\Rightarrow e=\dfrac{\sqrt{5}}{5} $ .
Phương trình đường chuẩn $ \Delta :x=\pm \dfrac{a}{e}\Rightarrow x=\pm \dfrac{5}{\dfrac{\sqrt{5}}{5}}=\pm 5\sqrt{5} $ .
Câu 3: Cho elip $ \dfrac{{{x}^{2}}}{25}+\dfrac{{{y}^{2}}}{9}=1 $ độ dài trục lớn, trục nhỏ lần lượt là :
- A
- B
- C
- D
Độ dài trục lớn là $ 2a=10 $
Độ dài trục bé là: $ 2b=6 $
Câu 4: Đường Elip $ \dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{7}=1 $ có tiêu cự bằng
- A
- B
- C
- D
Ta có $ {{c}^{2}}={{a}^{2}}-{{b}^{2}}=9\Rightarrow c=3 $ suy ra
tiêu cự: $ 2c=6 $ .
Câu 5: Cho elip $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ , phương trình đường chuẩn là :
- A
- B
- C
- D
Phương trình đường chuẩn của elip là : $ \Delta :x=\pm \dfrac{a}{e} $
Câu 6: Cho elip $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ tâm sai của elip là :
- A
- B
- C
- D
Tâm sai $ e=\dfrac{c}{a} $ với $ {{b}^{2}}={{a}^{2}}-{{c}^{2}} $
Câu 7: Elip $ \dfrac{{{x}^{\text{2}}}}{\text{9}}\text{+}\dfrac{{{y}^{\text{2}}}}{\text{5}}=1 $ có một tiêu điểm là
- A
- B
- C
- D
Từ dạng của elip $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ ta có $ \left\{ \begin{array}{l} & a=3 \\ & b=\sqrt{5} \end{array} \right. $ .
Từ công thức $ {{b}^{2}}={{a}^{2}}-{{c}^{2}}\Rightarrow c=2\Rightarrow {{F}_{1}}\left( -2;0 \right),{{F}_{2}}\left( 0;2 \right) $
Câu 8: Đường Elip $ \dfrac{{{x}^{2}}}{9}+\dfrac{{{y}^{2}}}{6}=1 $ có 1 tiêu điểm là
- A
- B
- C
- D
Ta có: $ {{c}^{2}}={{a}^{2}}-{{b}^{2}}=3\Rightarrow c=\sqrt{3} $ suy ra tiêu điểm $ F\left( \pm \sqrt{3};0 \right) $ .
Câu 9: Cho elip $ \dfrac{{{x}^{2}}}{{{3}^{2}}}+\dfrac{{{y}^{2}}}{{{2}^{2}}}=1 $ độ dài trục lớn, trục nhỏ lần lượt là :
- A
- B
- C
- D
Độ dài trục lớn là $ 2a=6 $
Độ dài trục bé là: $ 2b=4 $
Câu 10: Tâm sai của elip $ \dfrac{{{x}^{\text{2}}}}{\text{5}}\text{+}\dfrac{{{y}^{\text{2}}}}{\text{4}}=1 $ bằng
- A
- B
- C
- D
Từ dạng của elip $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ ta có $ \left\{ \begin{array}{l} & a=\sqrt{5} \\ & b=2 \end{array} \right. $ .
Từ công thức $ {{b}^{2}}={{a}^{2}}-{{c}^{2}}\Rightarrow c=1 $ .
Tâm sai của elip $ e=\dfrac{c}{a}\Rightarrow e=\dfrac{1}{\sqrt{5}}=\dfrac{\sqrt{5}}{5} $ .
Câu 11: Tâm sai của elip $ \dfrac{{{x}^{\text{2}}}}{\text{16}}\text{+}\dfrac{{{y}^{\text{2}}}}{9}=1 $ là:
- A
- B
- C
- D
Từ dạng của elip $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ ta có $ \left\{ \begin{array}{l} & a=4 \\ & b=3 \end{array} \right. $ .
Từ công thức $ {{b}^{2}}={{a}^{2}}-{{c}^{2}}\Rightarrow c=\sqrt{7} $ .
Tâm sai của elip $ e=\dfrac{c}{a}\Rightarrow e=\dfrac{\sqrt{7}}{4} $ .