Định nghĩa tích vô hướng cả hai vectơ
Lý thuyết về Định nghĩa tích vô hướng cả hai vectơ
Định nghĩa tích vô hướng cả hai vectơ
Tích vô hướng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$là một số, kí hiệu $\overrightarrow{a}.\overrightarrow{b}$, được xác định bởi
$\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|.\cos \left( \overrightarrow{a,}\overrightarrow{b} \right)$
Ví dụ:
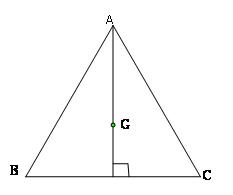
Cho tam giác đều ABC có cạnh a và trọng tâm G .Tính các tích vô hướng sau
$\begin{align}& \overrightarrow{AB}.\overrightarrow{AC};\overrightarrow{AC}.\overrightarrow{CB};\overrightarrow{AG}.\overrightarrow{AB} \\ &\overrightarrow{GB}.\overrightarrow{GC};\overrightarrow{BG}.\overrightarrow{GA};\overrightarrow{GA}.\overrightarrow{BC} \\ \end{align}$
Giải.
Theo định nghĩa ta có
$\begin{align}& \overrightarrow{AB}.\overrightarrow{AC}=a.a.\cos {{60}^{o}}=\dfrac{1}{2}{{a}^{2}} \\ & \overrightarrow{AC}.\overrightarrow{CB}=a.a.\cos {{120}^{o}}=-\dfrac{1}{2}{{a}^{2}} \\ & \overrightarrow{AG}.\overrightarrow{AB}=a\dfrac{\sqrt[{}]{3}}{3}.a.\cos {{30}^{o}}={{a}^{2}}\dfrac{\sqrt[{}]{3}}{3}.\dfrac{\sqrt[{}]{3}}{3}=\dfrac{1}{2}{{a}^{2}} \\ & \overrightarrow{GB}.\overrightarrow{GC}=a\dfrac{\sqrt[{}]{3}}{3}.a\dfrac{\sqrt[{}]{3}}{3}.\cos {{120}^{0}}=\dfrac{{{a}^{2}}}{6} \\ & \overrightarrow{BG}.\overrightarrow{GA}=a\dfrac{\sqrt[{}]{3}}{3}.a\dfrac{\sqrt[{}]{3}}{3}.\cos {{60}^{o}}=\dfrac{{{a}^{2}}}{6} \\ & \overrightarrow{GA}.\overrightarrow{BC}=a\dfrac{\sqrt[{}]{3}}{3}.a.\cos {{90}^{0}}=0 \\ \end{align}$
Bình phương vô hướng
Bình phương vô hương của một vectơ bằng bình phương độ dài của vectơ đó
Bài tập tự luyện có đáp án
Câu 1: Tính góc giữa hai vectơ $ \overrightarrow{a},\overrightarrow{b}$ biết $ \overrightarrow{a}.\overrightarrow{b}=\dfrac{1}{2}\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right| $ , ( $ \overrightarrow{a} $ , $ \overrightarrow{b} $ $ \ne \overrightarrow{0} $ ).
- A
- B
- C
- D
$\begin{array}{l} \vec a.\vec b = \frac{1}{2}\left| {\vec a} \right|.\left| {\vec b} \right|\\ \Leftrightarrow \left| {\vec a} \right|.\left| {\vec b} \right|\cos \left( {\vec a,\vec b} \right) = \frac{1}{2}\left| {\vec a} \right|.\left| {\vec b} \right|\\ \Leftrightarrow \cos \left( {\vec a,\vec b} \right) = \frac{1}{2} \end{array}$
nên $ \left( \overrightarrow{a},\overrightarrow{b} \right)={{60}^{\text{o}}} $
Câu 2: Cho tam giác $ ABC $ vuông tại $ C $ có $ AC=9 $ , $ BC=5 $ . Tính $ \overrightarrow{AB}.\overrightarrow{AC} $
- A
- B
- C
- D
Ta có $ \overrightarrow{AB}.\overrightarrow{AC}=\left( \overrightarrow{AC}+\overrightarrow{CB} \right).\overrightarrow{AC}=\overrightarrow{AC}.\overrightarrow{AC}+\overrightarrow{CB}.\overrightarrow{AC}=\overrightarrow{AC}.\overrightarrow{AC}=81 $
Câu 3: Cho tam giác $ ABC $ có đường cao $ BH $ ( $ H $ ở trên cạnh $ AC $ ).Câu nào sau đây đúng
- A
- B
- C
- D
Ta có $ \overrightarrow{BA}.\overrightarrow{CA}=\left( \overrightarrow{BH}+\overrightarrow{HA} \right).\overrightarrow{CA}=\overrightarrow{BH}.\overrightarrow{CA}+\overrightarrow{HA}.\overrightarrow{CA}=\overrightarrow{HA}.\overrightarrow{CA}=AH.AC $