Định nghĩa hai vectơ bằng nhau
Lý thuyết về Định nghĩa hai vectơ bằng nhau
Hai vectơ bằng nhau
+ Mỗi vectơ đều có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ →ađược kí hiệu là |→a|
+ Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài.
Nếu hai vectơ →a và →b bằng nhau thì ta viết →a = →b
Chú ý : Theo định nghĩa trên thì các vectơ không đều nhau : →AA=→BB=→PP=.... Bởi vậy , từ nay các vectơ - không được kí hiệu chung là →0
Bài tập tự luyện có đáp án
Câu 1: Cho hình bình hành ABCD . Khẳng định nào sau đây là sai:
- A
- B
- C
- D
Giả sử: →AB+→AC=→AD⇔→AB+→AC=→BC⇔→AB=→BC−→AC=→BA (Vô lý)
Câu 2: Cho tứ giác ABCD . Nếu →AB=→DC thì ABCD là hình gì? Tìm đáp án đúng
- A
- B
- C
- D
→AB=→DC thì ABCD là hình bình hành
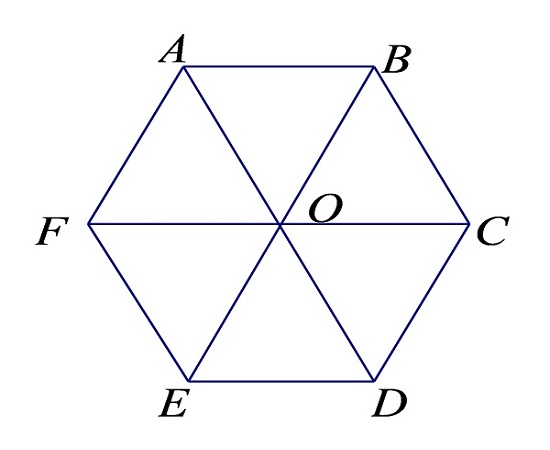
Câu 3: Cho lục giác đều ABCDEF có tâm O . Có bao nhiêu vectơ bằng vectơ →AB ?
- A
- B
- C
- D
Từ hình vẽ trên ta thấy các vectơ bằng vectơ →AB là: →FO , →OC và →ED .
Câu 4: Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn AB ?
- A
- B
- C
- D
Điều kiện cần và đủ để O là trung điểm AB là →OA+→OB=→0.
Câu 5: Cho hình thang cân ABCD có DC=2AB . E là trung điểm của DC . Khi đó, đẳng thức nào sau đây đúng?
- A
- B
- C
- D

E là trung điểm của DC nên ta có →DE=→EC.
Câu 6: Điều kiện nào là điều kiện cần và đủ để →AB=→CD là
- A
- B
- C
- D
Hai vecto bằng nhau khi chúng:
- Cùng độ dài
- Cùng hướng
Nên →AB=→CD⇔{|→AB|=|→CD|→AB↑↑→CD
Hay ABDC là hình bình hành
Câu 7: Hai vectơ bằng nhau khi chúng thỏa mãn điều kiện:
- A
- B
- C
- D
Theo định nghĩa, hai véc tơ bằng nhau khi chúng cùng hướng và cùng độ dài
Câu 8: Cho hình thoi ABCD,E là giao điểm hai đường chéo. Đẳng thức nào sau đây là sai?
- A
- B
- C
- D

AC,BD cắt nhau tại E ⇒→AC,→BD không cùng phương nên →AC=→BD là sai
Câu 9: Cho lục giác đều ABCDEF tâm O. Số vectơ bằng vecto →BA là:
- A
- B
- C
- D

Các vectơ bằng vecto →BA là: →BA;→OF;→DE;→CO
Câu 10: Cho hình bình hành ABCD tâm O. Véctơ bằng →OC là
- A
- B
- C
- D

Ta có O là trung điểm của AC nên →AO=→OC.
Câu 11: Chọn khẳng định đúng?
- A
- B
- C
- D
Hai vectơ bằng nhau nếu chúng cùng hướng và có cùng độ dài là khẳng định đúng.
Câu 12: Cho tam giác ABC , có tất cả bao nhiêu véctơ khác →0 có điểm đầu và điểm là 2 trong 3 đỉnh A,B,C trên.
- A
- B
- C
- D
Các véc tơ khác →0 lập được từ 2 trong 3 đỉnh A,B,C là →AB,→BA,→AC,→CA,→BC,→CB nên có 6 vectơ.
Câu 13: Cho tam giác ABC có trực tâm H và O là tâm đường tròn ngoại tiếp. Gọi B′ là điểm đối xứng của B qua O . Khi đó,
- A
- B
- C
- D

Vì H là trực tâm ΔABC⇒ CH⊥AB
Ta có ΔBAB′ vuông tại A⇒B′A⊥AB
Suy ra AB′//CH.
Mà lại có {AH⊥BCB′C⊥BC⇒AH//B′C.
Từ đó ta cóAHCB′ là hình bình hành.
Vậy →AH=→B′C.
Câu 14: Cho hình thang ABCD có AB//CD và CD=3AB . O là giao điểm hai đường chéo của hình thang. Trên OC,OD lần lượt lấy hai điểm I,J sao cho OIIC=OJJD=1k . Tìm giá trị của k để →AB=→JI ?
- A
- B
- C
- D

Theo giả thiết: OIIC=OJJD=1k⇒JI//DC//AB
→AB=→JI⇒AB=JI
Mà: CD=3AB⇒CD=3JI
Vì JI//DC nên xét tam giác OCD ta có: OIIC=OJJD=12
Câu 15: Cho N là trung điểm của đoạn OM . Vẽ đường tròn (O,ON) . Từ M kẻ hai tiếp tuyến đến (O) tiếp xúc với (O) lần lượt tại A,B . Mệnh đề nào sau đây sai?
- A
- B
- C
- D
+ ΔOAM vuông tại A có AN là trung tuyến ⇒ON=AN=NM.
+ OA=ON⇒OA=AN.
+ Tương tự ta có OB=BN.
+ OA=OB⇒OA=OB=AN=BN.
+ Suy ra OANB là hình thoi ⇒ →OA=−→NB.
Câu 16: Cho tứ giác ABCD nội tiếp (O).B′,D′ lần lượt là điểm đối xứng của B,D qua O . H là trực tâm tam giác BCD . Chọn khẳng định sai:
- A
- B
- C
- D
Ta có tam giác DD′C vuông tại C⇒D′C⊥DC
H là trực tâm tam giác BDC⇒BH⊥DC
⇒D′C//BH
Tương tự ta có CH//BD′
⇒BD′CH là hình bình hành
Hay →BD′=→HC
Câu 17: Cho N là trung điểm của đoạn OM . Vẽ đường tròn (O,ON) . Từ M kẻ hai tiếp tuyến đến (O) tiếp xúc với (O) lần lượt tại A,B . Để chứng minh →OA=→BN , một bạn học sinh đã làm như sau:
Bước 1: ΔOAM vuông tại A có AN là trung tuyến ⇒ON=AN=NM
Bước 2: OA=ON⇒OA=AN
Bước 3: Tương tự bước 1, bước 2 ta có OB=BN
Bước 4: OA=OB⇒OA=OB=AN=BN
Bước 5: Suy ra: OANB là hình thoi ⇒
→OA=→BN
Bài giải của bạn học sinh trên:
- A
- B
- C
- D
Vẽ hình quan sát ta thấy các bước lời giải đều đúng

Câu 18: Cho tam giác ABC . Trên cạnh AC lấy điểm E sao cho AC=3AE. Kẻ EF//AB (F∈BC) . Trên đoạn AB lấy điểm I sao cho →AI=→EF. Khi đó khẳng định nào sau đây là đúng?
- A
- B
- C
- D

Ta có EF//AB⇒AI và EF cùng phương
Để →AI=→EF thì |→AI|=|→EF|
Hay AEFI là hình bình hành.
⇒IF//AC⇒BIBA=BFBC=13⇒→AI=−2→BI.
Câu 19: Cho hình bình hành ABCD tâm O có ^ADC=60∘ . Trên DA lấy E sao cho →AD=−53→AE . EO∩BC=F . Điều kiện để DEBF là hình chữ nhật là:
- A
- B
- C
- D

Ta có: {AO=OCEO=OF^AOE=^COF⇒ΔAEO=ΔCFO (c-g-c)
⇒AE=CF⇒ED=FB
Hay DEBF là hình bình hành
Để DEBF là hình chữ nhật thì ^AEB=90∘
Mà ^ADC=60∘⇒⌢EAB=60∘ ( AB//CD ) ⇒AB=2AE ( ΔAEB vuông tại E)
Lại có AD=53AE⇒ABAD=65