Xét một đoạn mạch xoay chiều mắc nối tiếp gồm cuộn dây D và tụ điện C.

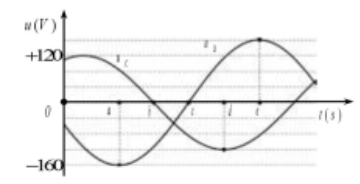
Xét một đoạn mạch xoay chiều mắc nối tiếp gồm cuộn dây D và tụ điện C. Điện áp tức thời ở hai đầu cuộn dây D và điện áp tức thời ở hai đầu tụ điện C được biểu diễn bởi các đồ thị $\Large u_D,u_C$ như hình vẽ. Trên trục thời gian t, khoảng cách giữa các điểm a - b, b - c, c - d, d - e là bằng nhau. Điện áp hiệu dụng ở hai đầu đoạn mạch gần nhất với giá trị nào sau đây? 

• A. 200 V
• B. 80 V
• C. 140 V
• D. 40 V

Phương pháp: 
Sử dụng kĩ năng đọc đồ thị 
Điện áp giữa hai đầu đoạn mạch: $\Large u=u_C+u_D$
Điện áp hiệu dụng giữa hai đầu đoạn mạch: $\Large U^{2}=U_C^{2}+U_D^{2}+2U_CU_D.\cos\Delta \varphi_{CD}$
Cách giải: 
Từ đồ thị ta thấy khoảng thời gian từ a đến e là $\Large \dfrac{T}{2}$

$\Large \Rightarrow t_{ab}=t_{bc}=t_{cd}=t_{de}=\dfrac{t_{ae}}{4}=\dfrac{T}{8}$

$\Large \Rightarrow \varphi_{ab}=\varphi_{bc}=\varphi_{cd}=\varphi_{de}=\dfrac{\pi}{4}(rad)$
Tại thời điểm $\Large d,u_C=-U_{0C}=-120(V)$ 
Ta có vòng tròn lượng giác: 
 
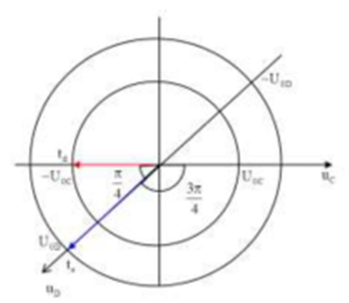
Từ vòng tròn lượng giác, ta thấy ở thời điểm $\Large e,u_D=U_{0D}=160(V)$
$\Large \rightarrow$ độ lệch pha giữa $\Large u_D$ và $\Large u_C$ là: $\Large \varphi_{CD}=\dfrac{3\pi}{4}rad$ 
Điện áp cực đại giữa hai đầu đoạn mạch là: 

$\Large U_0^{2}=U_{0C}^{2}+U_{0D}^{2}=2U_{0C}U_{0D}.\cos\Delta \varphi_{CD}$

$\Large \Rightarrow U_0^{2}=120^{2}+160^{2}+2.120.160.\cos\dfrac{3\pi}{4}$

$\Large \Rightarrow U_0 = 113,3(V)\Rightarrow U=\dfrac{113,3}{\sqrt{2}}=80,1(V)$
Chọn B.